Question

What is Binary search? Discuss with example.

Answer 1

Binary Search:
Binary search also called half–interval search algorithm. It finds the position of a search element within a sorted array. The binary search algorithm can be done as a divide-and-conquer search algorithm and executes in logarithmic time.

Pseudocode for Binary search:

(I) Start with the middle element:

• If the search element is equal to the middle element of the array i.e., the middle value = number of elements in array/2, then return the index of the middle element.
• If not, then compare the middle element with the search value,
• If the search element is greater than the number in the middle index, then select the elements to the right side of the middle index, and go to Step-1.
• If the search element is less than the number in the middle index, then select the elements to the left side f the middle index, and start with Step-1.

(II) When a match is found, display a success message with the index of the element matched.
(III) If no match is found for all comparisons, then display an unsuccessful message.

Binary Search Working principles:

The list of elements in an array must be sorted first for Binary search. The following example describes the step-by-step operation of binary search. Consider the following array of elements, the array is being sorted so it enables to do the binary search algorithm. Let us assume that the search element is 60 and we need to search the location or index of search element 60 using binary search.

First, we find an index of the middle element of the array by using this formula:
mid = low + (high – low) / 2
Here it is, 0 + (9 – 0 ) / 2 = 4 (fractional part ignored). So, 4 is the mid value of the array.

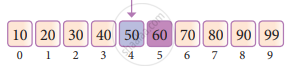
Now compare the search element with the value stored at mid-value location 4. The value stored at the location or index 4 is 50, which is not match the search element. As the search value of 60 is greater than 50.

Now we change our low to mid + 1 and find the new mid-value again using the formula, low to mid – 1
mid = low + (high – low) / 2
Our new mid is 7 now. We compare the value stored at location 7 with our target value of 31.

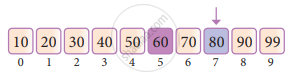
The value stored at the location or index 7 is not a match with the search element, rather it is more than what we are looking for. So, the search element must be in the lower part of the current mid-value location.

The search element still not found. Hence, we calculated the mid again by using the formula.
high = mid – 1
mid = low + (high – low) / 2
Now the mid-value is 5.

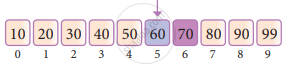
Now we compare the value stored at location 5 with our search element. We found that it is a match.

We can conclude that the search element 60 is found at the location or index 5. For example, if we take the search element as 95, For this value this binary search algorithm returns an unsuccessful result.