Advertisements
Advertisements
Question
With a neat labelled diagram, explain cyclotron motion and cyclotron formula.
Solution
Assume that a particle with mass m and charge q moves into an area where a uniform magnetic field of induction `vec(B)` is present. `vec(B)` is pointing to the page in the figure. The particle's velocity, `vec(v)`, and the magnetic force, `vec(F)_m`, are always perpendicular to one another. The charged particle moves in a uniform circular motion in the magnetic field, with the magnetic force supplying the centripetal acceleration, assuming that it began its journey in a plane perpendicular to `vec(B)`.
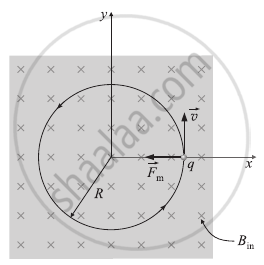
Charge q moving anticlockwise in a plane perpendicular to lB into the page
If the charge moves in a circle of radius R,
`F_m = |q|vB = (mv^2)/R`
∴ mv = p = |q| BR ...(1)
where p = mv is the linear momentum of the particle. Equation (1) is known as the cyclotron formula because it describes the motion of a particle in a cyclotron – the first of the modern particle accelerators.
