Question

With the help of a neat labelled diagram, obtain an expression for the induced emf in a stationary coil in a changing magnetic field.

Answer 1

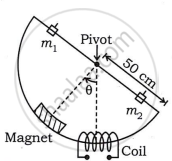
Fig. (a): Magnet-coil system

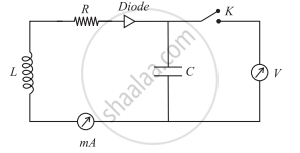
Fig. (b) : Measurement of induced emf

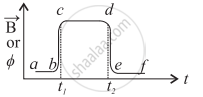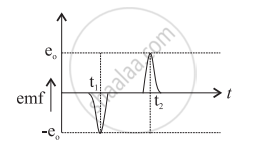Fig. (c): Variation of `vecB` with time t,	Fig. (d): Variation of e with time t.

A permanent bar magnet is installed on an arc of a semicircle with a radius of 50 cm in a magnet-coil system, as shown in fig. (a). The arc is part of a robust aluminium frame and is suspended in the core of the arc so that the entire system can oscillate freely in its plane. A coil of around 10,000 turns of copper wire loops the arc, allowing the bar magnet to freely move over it.

A capacitor (C) and a diode (D) are connected across the coil to detect the induced emf [Fig. (b)]. As the magnet in the middle of the arc [Fig. (a)] advances across it and recedes, the magnetic flux through the coil changes from a small value to a maximum and then back to a small value, inducing an emf.

The variation of magnetic field `vecB` ·(at the coil in mean position) with time is shown in Fig. (c).

`e = - (dphi)/dt`     ...from Lenz' law

It follows that emf (e) is 'negative' when Φ increases at time t₁ and 'positive' when Φ decreases at time t₂.

The diode in fig. (b) will only conduct during the positive pulse. The capacitor will charge to a potential of e₁ during the first half swing. There is no conduction in the next half until the next positive pulse arrives and charges the capacitor to e₂. This continues until the voltage/emf pulse charges the capacitor to its max value e₀.

The equation for induced emf can be written as,

`e = |(dphi)/dt| = |(dphi)/ (dθ)| . |(dθ)/dt|`    ...(i)

At θ = 0, the mean position, Φ is maximum.

`(dphi)/dt =` 0 at θ = 0

The seconf term `(dθ)/dt` can be deduced from the equation,

`θ = θ_0 sin 2pi vt`

where, θ₀ = amplitude of oscillating magnet Frequency, `v= 1/"time period (T)"`

∴ `θ = θ_0 sin  (2pi)/Tt`

∴ `(dθ)/ dt = θ_0 cos  (2pi)/T t ((2pi)/T)`

  ∴ `(dθ) /dt = (2piθ_0)/T. cos  ((2pit)/ T)`      ....(ii)

`|e_0| = ((dphi)/dt)_max = ((dphi)/(dθ))_max. ((2piθ_0)/T)`   ....(iii)

The peak induced emf e₀ for a particular magnet-coil system is directly related to angular amplitude (θ_o)and inversely proportional to time period. (T).