Advertisements
Advertisements
Question
Without actually performing the long division, state whether state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
Solution
The given number is \[\frac{129}{2^2 \times 5^7 \times 7^{17}}\]
Clearly, none of 2, 5 and 7 is a factor of 129.
So, the given number is in its simplest form.
Now,
APPEARS IN
RELATED QUESTIONS
Write a rational number between`sqrt(3)` and 2
Without actually performing the long division, state whether state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion.
Write down the decimal expansions of the following rational numbers by writing their denominators in the form 2m × 5n, where, m, n are non-negative integers.\[\frac{14588}{625}\]
What can you say about the prime factorisations of the denominators of the following rationals: 0.120120012000120000 ...
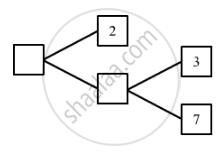
Complete the missing entries in the following factor tree.
Has the rational number \[\frac{441}{2^2 \times 5^7 \times 7^2}\] a terminating or a nonterminating decimal representation?
Write whether \[\frac{2\sqrt{45} + 3\sqrt{20}}{2\sqrt{5}}\]
on simplification gives a rational or an irrational number.
State whether the following rational number will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
`77/210`
Write down the decimal expansion of the following number which have terminating decimal expansion.
`35/50`
Find after how many places of decimal the decimal form of the number `27/(2^3. 5^4. 3^2)` will terminate.
