Advertisements
Advertisements
Questions
Write Einstein's photoelectric equation and mention which important features in photoelectric effect can be explained with the help of this equation.
The maximum kinetic energy of the photoelectrons gets doubled when the wavelength of light incident on the surface changes from λ1 to λ2. Derive the expressions for the threshold wavelength λ0 and work function for the metal surface.
State two important features of Einstein's photoelectric equation.
Solution
Einstein's photoelectric equations is given by
`K_max=1/2mv_max^2=hv=phi_0`
where
Kmax = Maximum kinetic energy of the photoelectron
vmax = Maximum velocity of the emitted photoelectron
m = Mass of the photoelectron
ν = Frequency of the light radiation
ϕ0 = Work function
If ν0 is the threshold frequency, then the work function can be written as
ϕ0 = hν0
`=>K_max=1/2mv_max^2=hv-hv_0=h(v-v_0)`
The above equations explains the following results:
1. If ν < ν0, then the maximum kinetic energy is negative, which is impossible. Hence, photoelectric emission does not take place for the incident radiation below the threshold frequency. Thus, the photoelectric emission can take place if ν > ν0.
2. The maximum kinetic energy of emitted photoelectrons is directly proportional to the frequency of the incident radiation. This means that maximum kinetic energy of photoelectron depends only on the frequency of incident light.
According to the photoelectric equation,
`K_max=1/2mv_max^2=hv-phi_0`
`K_max=(hc)/lambda_1-phi_0`
Let the maximum kinetic energy for the wavelength of the incident λ2 be K'max
`K'_max=(hc)/lambda_2-phi_0`
Form (i) and (ii), we have
`(hc)/lambda_2-phi_0=2((hc)/lambda_1-phi_0)`
`=>phi_0=hc(2/lambda_1-1/lambda_2)`
`=>hv_0=hc(2/lambda_1-1/lambda_2)`
`=>c/(lambda_0)=c(2/lambda_1-1/lambda_2)`
`=>1/lambda_0=(2/lambda_1-1/lambda_2)`
`=>lambda_0=((lambda_1lambda_2)/(2lambda_2-lambda_1))`
APPEARS IN
RELATED QUESTIONS
The momentum of a photon of de Broglie wavelength 5000Å is _______.
[Planck’s constant = 6.63 x10-34 J.s.]
According to Einstein’s model, the threshold frequency for a metal having work function ϕ0 is given by _________.
Calculate the maximum kinetic energy of photoelectrons emitted by a metal (work function = 1.5 eV) when it is illuminated with light of wavelength 198 nm.
A police van moving on a highway with a speed of 30 km/h fires a bullet at a thief's car speeding away in the same direction with a speed of 192 km/h. If the muzzle speed of the bullet is 150 m is, with what speed does the bullet hit the thief's car?
In an inelastic collision, which of the following does not remain conserved?
Radiations of two photon's energy, twice and ten times the work function of metal are incident on the metal surface successively. The ratio of maximum velocities of photoelectrons emitted in two cases is:
Who indirectly determined the mass of the electron by measuring the charge of the electrons?
If the energy of photon corresponding to a wavelength of 6000 A° is 3.32 × 10-19 J, the photon energy for a wavelength of 4000 A° will be
- Calculate the energy and momentum of a photon in a monochromatic beam of wavelength 331.5 nm.
- How fast should a hydrogen atom travel in order to have the same momentum as that of the photon in part (a)?
The graphs below show the variation of the stopping potential VS with the frequency (ν) of the incident radiations for two different photosensitive materials M1 and M2.
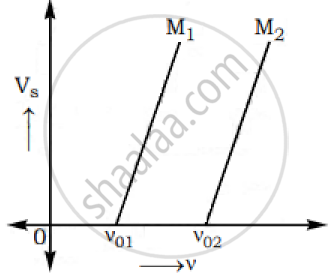
Express work function for M1 and M2 in terms of Planck’s constant(h) and Threshold frequency and charge of the electron (e).
If the values of stopping potential for M1 and M2 are V1 and V2 respectively then show that the slope of the lines equals to `(V_1-V_2)/(V_(01)-V_(02))` for a frequency,
ν > ν02 and also ν > ν01
