Advertisements
Advertisements
Question
यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो इसके पृष्ठीय क्षेत्रफल में कितने गुना वृद्धि होगी?
Solution
माना, घन की भुजा = l
तब पुराने घन का पृष्ठीय क्षेत्रफल = 6l2 ...(i)
यदि घन के प्रत्येक किनारे को दुगुना कर दिया जाए तो भुजा = 2 × l
तब नए घन का पृष्ठीय क्षेत्रफल = 6(2l)2 = 6 × 4l2
= 4 × 6l2 ....(ii)
समीकरण (i) व (ii) से
नए घन का पृष्ठीय क्षेत्रफल = 4 × पुराने घन का पृष्ठीय क्षेत्रफल
अतः इस स्थिति में घन का पृष्ठीय क्षेत्रफल चार गुना हो जाएगा।
APPEARS IN
RELATED QUESTIONS
यदि किसी घन के प्रत्येक किनारे को दुगुना कर दिया जाए, तो इसके आयतन में कितने गुना वृद्धि होगी?
एक कुंड के अंदर 60 लीटर प्रति मिनट की दर से पानी गिर रहा है। यदि कुंड का आयतन 108 m3 है, तो ज्ञात कीजिए कि इस कुंड को भरने में कितने घंटे लगेंगे?
तुम्हारे घन का किनारा कितना लंबा है? _____
कितने सेंटीमीटर घन उसकी
- लंबाई है? ______
- चौड़ाई है? ______
- ऊचाँई है? ______
थिम्पू के प्रश्नो के उत्तर दो:
- मेज़ पर पहली परत बनाने के लिए मुझे कितने cm घनों का इस्तेमाल करना होगा?

- पूरा घन बनाने के लिए ऐसी कितनी परतें मुझे बनानी पड़ेंगी?

कुल उपयोग में लाए गए सेंटीमीटर घन होंगे = ______?
कागजी घन का आयतन ______ सेंटीमीटर घनों के बराबर है।
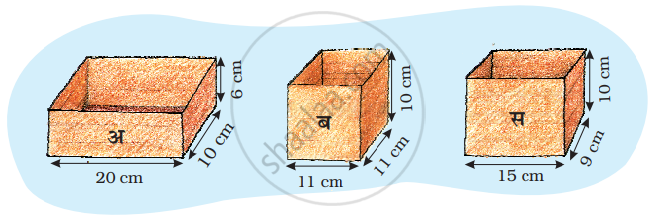
गणेश और डिंगा 4000 सेंटीमीटर घनों को बक्सों में पैक करना चाहते हैं। घनों को एक स्कूल में भेजा जाना है। तीन अलग- अलग तरह के बक्से पेकिंग के लिए मिले हुए हैं।
 |
|
| क्या हम 4000 घन इन तीन बक्सों में सही से पैक कर पाएँगे? मुझे लगता है हमें एक और बक्से की ज़रूरत होगी। | मुझे लगता है कि इन तीन बक्सों में इन घनों के लिए बहुत जगह है। |
 |
|
तुम्हारा क्या अंदाज़ा है? कौन सही है?
गणेश और डिंगा 4000 सेंटीमीटर घनों को बक्सों में पैक करना चाहते हैं। घनों को एक स्कूल में भेजा जाना है। तीन अलग- अलग तरह के बक्से पेकिंग के लिए मिले हुए हैं।
 |
|
| क्या हम 4000 घन इन तीन बक्सों में सही से पैक कर पाएँगे? मुझे लगता है हमें एक और बक्से की ज़रूरत होगी। | मुझे लगता है कि इन तीन बक्सों में इन घनों के लिए बहुत जगह है। |
 |
|
गणेश के तरीके से पता लगाओ:
- बॉक्स ब में कितने घनों को लगाया जा सकता है? ______
- बॉक्स स में कितने घनों को लगाया जा सकता है? ______
- तो कुल मिलाकर तीनो बक्सों में कितने घन आ सकते हैं? ______
एक घन का कुल पृष्ठीय क्षेत्रफल 96 cm2 है। घन का आयतन है :
