Advertisements
Advertisements
The following is a function of class Armstrong. This recursive function calculates and returns the sum of the cubes of all the digits of num, where num is an integer data member of the class Armstrong.
[A number is said to be Armstrong if the sum of the cubes of all its digits is equal to the original number].
There are some places in the code marked by ?1?, ?2?,?3? which may be replaced by a statement/expression so, that the function works properly.
public int sumOfPowers(int num)
{
if(num == 0)
return ?1?
int digit = ?2?;
return(int)Math.pow(digit, 3) + ?3?;
}
- What is the expression or statement at ?1?
- What is the expression or statement at ?2?
- What is the expression or statement at ?3?
Concept: undefined > undefined
A class LCM has been defined to find the Lowest Common Multiple of two integers.
Some of the data members and member functions are given below:
| Class name | LCM |
| Data members/instance variables: |
|
| n1 | to store an integer number |
| n2 | to store an integer number |
| large | integer to store the largest from n1,n2 |
| sm | integer to store the smallest from n1,n2 |
| l | to store lcm of two numbers |
| Methods / Member functions: | |
| LCM( ) | default constructor to initialize data members with legal initial values |
| void accept() | to accept n1 and n2 |
| int getLCM() | returns the lcm of n1 and n2 using the recursive technique |
| void display( ) | to print the numbers n1, n2 and lcm |
Specify the class LCM giving details of the constructor( ), void accept( ), int getLCM() and void display( ). Define a main ( ) function to create an object and call the member functions accordingly to enable the task.
Concept: undefined > undefined
Advertisements
The following function is a part of some class which is used to find the smallest digit present in a number. There are some places in the code marked by ?1?, ?2?, ?3? which must be replaced by an expression/a statement so that the function works correctly.
int small_dig(int n)
{ int min=?1?;
while(n!=0)
{
int q=n/10;
int r=?2?*10;
min=r>min ? ?3? : r;
n=q;
}
return min;
}
- What is the expression or statement at ?1?
- What is the expression or statement at ?2?
- What is the expression or statement at ?3?
Concept: undefined > undefined
Recycle is an entity which can hold at the most 100 integers. The chain enables the user to add and remove integers from both the ends i.e. front and rear.
Define a class ReCycle with the following details:
| Class name | ReCycle |
| Data members/instance variables: | |
| ele[ ] | the array to hold the integer elements |
| cap | stores the maximum capacity of the array |
| front | to point the index of the front |
| rear | to point the index of the rear |
| Methods / Member functions: | |
| ReCycle (int max) | constructor to initialize the data cap = max, front = rear = 0 and to create the integer array. |
| void pushfront(int v) | to add integers from the front index if possible else display the message(“full from front”). |
| int popfront( ) | to remove the return elements from front. If array is empty then return-999 |
| void pushrear(int v) | to add integers from the front index if possible else display the message(“full from rear”). |
| int poprear( ) | to remove and return elements from rear. If the array is empty then return-999. |
- Specify the class ReCycle giving details of the functions void pushfront(int) and int poprear( ). Assume that the other functions have been defined.
The main( ) function and algorithm need NOT be written. - Name the entity described above and state its principle.
Concept: undefined > undefined
Convert the following infix notation to postfix notation:
A * (B + C / D ) – E / F Concept: undefined > undefined
Convert the following infix notation to postfix form.
(P + Q * R - S)/T * U
Concept: undefined > undefined
With the help of an example, briefly explain the dominant term in complexity.
Concept: undefined > undefined
Convert the following infix notation to prefix form.
( A – B ) / C * ( D + E )
Concept: undefined > undefined
From the given logic diagram:

- Derive Boolean expression and draw the truth table for the derived expression
- If A=1, B=0 and C=1, then find the value of X.
Concept: undefined > undefined
Verify if the following proposition is valid using the truth table:
(X ∧ Y) =>Z = (Y => Z) ∧ (X => Y).
Concept: undefined > undefined
Answer the following question on the diagram of a Binary Tree given below:
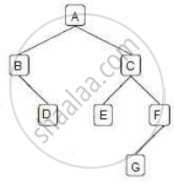
State the degree of the nodes C and G. Also, state the level of these nodes when the root is at level 0.
Concept: undefined > undefined
Answer the following question on the diagram of a Binary Tree given below:

Write the pre-order and post-order traversal of the above tree structure.
Concept: undefined > undefined
Answer the following questions based on the diagram of a Binary Tree given below:
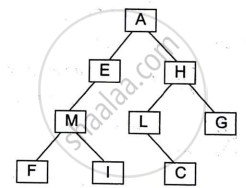
- Name the external nodes of the tree.
- State the degree of node M and node L.
- Write the post-order traversal of the above tree structure.
Concept: undefined > undefined
A linked list is formed from the objects of the class Node. The class structure of the Node is given below:
class Node
{
int n;
Node link;
}
Write an Algorithm OR a Method to search for a number from an existing linked list. The method declaration is as follows:
void FindNode( Node str, int b)
Concept: undefined > undefined
Answer the following questions from the diagram of a Binary Tree given below:
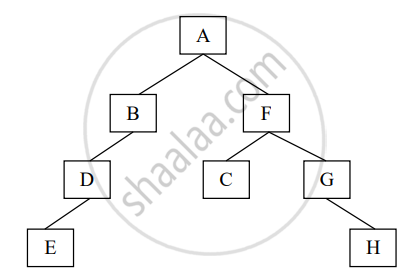
- Name the root of the left sub tree and its siblings.
- State the size and depth of the right sub tree.
- Write the in-order traversal of the above tree structure.
Concept: undefined > undefined
For Big O notation, state the difference between O(n) and O(n2 ).
Concept: undefined > undefined
The ability of an object to take many forms is known as ______.
Concept: undefined > undefined
According to the Principle of duality, the Boolean equation
(A+ B') • (A+ 1) =A+ B' will be equivalent to ______.
Concept: undefined > undefined
Verify if the following proposition is a Tautology, Contradiction or Contingency using a truth table.
((A=>B)∧(B=>C))=>(A=>C)
Concept: undefined > undefined
Find the complement of the following expression and reduce it by using Boolean laws.
P•( 13 ± Q)•Q•(Q+R')
Concept: undefined > undefined
