Topics
Sets and Relations
- Introduction of Set
- Representation of a Set
- Intervals
- Types of Sets
- Operations on Sets
- Relations of Sets
- Types of Relations
Functions
- Concept of Functions
- Types of Functions
- Representation of Function
- Graph of a Function
- Fundamental Functions
- Algebra of Functions
- Composite Function
- Inverse Functions
- Some Special Functions
Complex Numbers 33
- Introduction of Complex Number
- Imaginary Number
- Concept of Complex Numbers
- Conjugate of a Complex Number
- Algebraic Operations of Complex Numbers
- Square Root of a Complex Number
- Solution of a Quadratic Equation in Complex Number System
- Cube Root of Unity
Sequences and Series
- Concept of Sequences
- Geometric Progression (G.P.)
- General Term Or the nth Term of a G.P.
- Sum of the First n Terms of a G.P.
- Sum of Infinite Terms of a G. P.
- Recurring Decimals
- Harmonic Progression (H. P.)
- Types of Means
- Special Series (Sigma Notation)
Locus and Straight Line
- Locus
- Equation of Locus
- Line
- Equations of Lines in Different Forms
- General Form Of Equation Of Line
Determinants
- Determinants
- Properties of Determinants
- Application of Determinants
- Determinant method
- Consistency of Three Linear Equations in Two Variables
- Area of a Triangle Using Determinants
- Collinearity of Three Points
Limits
- Definition of Limit of a Function
- Algebra of Limits
- Evaluation of Limits
- Direct Method
- Factorization Method
- Rationalization Method
- Limits of Exponential and Logarithmic Functions
Continuity
- Continuous and Discontinuous Functions
- Continuity of a Function at a Point
- Definition of Continuity
- Continuity from the Right and from the Left
- Properties of Continuous Functions
- Continuity in the Domain of the Function
- Examples of Continuous Functions Whereever They Are Defined
Differentiation
- The Meaning of Rate of Change
- Definition of Derivative and Differentiability
- Derivative by the Method of First Principle
- Rules of Differentiation (Without Proof)
- Applications of Derivatives
Partition Values
- Concept of Median
- Partition Values
- Quartiles
- Deciles
- Percentiles
- Relations Among Quartiles, Deciles and Percentiles
- Graphical Location of Partition Values
Measures of Dispersion
- Measures of Dispersion
- Range of Data
- Quartile Deviation (Semi - Inter Quartile Range)
- Variance and Standard Deviation
- Standard Deviation for Combined Data
- Coefficient of Variation
Skewness
- Skewness
- Asymmetric Distribution (Positive Skewness)
- Asymmetric (Negative Skewness)
- Measures of Skewness
- Karl Pearson’S Coefficient of Skewness (Pearsonian Coefficient of Skewness)
- Features of Pearsonian Coefficient
- Bowley’s Coefficient of Skewness
Bivariate Frequency Distribution and Chi Square Statistic
- Bivariate Frequency Distribution
- Classification and Tabulation of Bivariate Data
- Marginal Frequency Distributions
- Conditional Frequency Distributions
- Categorical Variables
- Contingency Table
- Chi-Square Statistic ( χ2 )
Correlation
- Correlation
- Concept of Covariance
- Properties of Covariance
- Concept of Correlation Coefficient
- Scatter Diagram
- Interpretation of Value of Correlation Coefficient
Permutations and Combinations
- Introduction of Permutations and Combinations
- Fundamental Principles of Counting
- Concept of Addition Principle
- Concept of Multiplication Principle
- Concept of Factorial Function
- Permutations
- Permutations When All Objects Are Distinct
- Permutations When Repetitions Are Allowed
- Permutations When All Objects Are Not Distinct
- Circular Permutations
- Properties of Permutations
- Combination
- Properties of Combinations
Probability
- Introduction of Probability
- Types of Events
- Algebra of Events
- Elementary Properties of Probability
- Addition Theorem of Probability
- Conditional Probability
- Multiplication Theorem on Probability
- Independent Events
Linear Inequations
- Linear Inequality
- Solution of Linear Inequality
- Graphical Representation of Solution of Linear Inequality in One Variable
- Graphical Solution of Linear Inequality of Two Variable
- Solution of System of Linear Inequalities in Two Variables
Commercial Mathematics
- Percentage
- Profit and Loss
- Simple and Compound Interest (Entrance Exam)
- Depreciation
- Partnership
- Goods and Service Tax (GST)
- Shares and Dividends
- Function, Domain, Co-domain, Range
- Types of function
1. One-one or One to one or Injective function
2. Onto or Surjective function - Representation of Function
- Graph of a function
- Value of funcation
- Some Basic Functions - Constant Function, Identity function, Power Functions, Polynomial Function, Radical Function, Rational Function, Exponential Function, Logarithmic Function, Trigonometric function
Definition
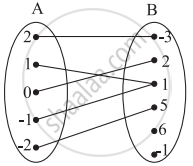
A relation f from a set A to a set B is said to be a function if every element of set A has one and only one image in set B.
A function which has either R or one of its subsets as its range is called a real valued function. Further, if its domain is also either R or a subset of R, it is called a real function.
Notes
In other words, a function f is a relation from a non-empty set A to a non-empty set B such that the domain of f is A and no two distinct ordered pairs in f have the same first element.
If f is a function from A to B and (a, b) ∈ f, then f (a) = b, where b is called the image of a under f and a is called the preimage of b under f.
The function f from A to B is denoted by f: A → B.
A funcion is a connection between 2 sets A and B f: A→B such that
1) All elements in A are associated to some element in B
2) This association is unique, that means one and only one.
Let's try to understand this with a simple anology,
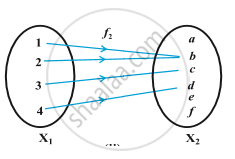
Here, let's say `"X"_1` is a set of all children and `"X"_2` is a set of all womens. And `"X"_1` and `"X"_2` have connection as mother and children.
So as per the definition there is a connention between 2 sets `"X"_1` and `"X"_2` such that all the elements of `"X"_1` are associated to some element in set `"X"_2` i.e all the childrens are related to a particualr mother, and this association is unique because no one child can have two or more mothers, but a mother can have more than one child.
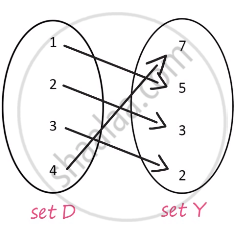
Consider the sets D and Y related to each ther as shown, clearly every element in the set D is related to exactly one element in the set Y. So the given relation is a function. f: D → Y.
Here, D is the domain of the function and Y is the co domain of the function.
f(1)= 5
Here, 5 is called the image of 1 under f and 1 is called preimage of 5 under f.
The range of this function is, Range= {2,3,5,7}
The range is a set of real numbers so the function is Real valued function.