Topics
Operating System
- Introduction to Operating System (OS)
- Idea of an Operating System
- Windows NT
- LINUX
- File Systems and Its types
- File Operations
- Access Methods and its types
- Allocation Methods
- Concepts Related to Process Management
- Concepts related to memory management
- Basics of Graphical User Interface (GUI)
- Access and Security Aspects of O.S.
Data Structures
C++ Programming
- Introduction to C++ Programming
- Idea Behind Object-Orientated Programming
- Object-orientated programming approach
- Object-Oriented Terms and Concepts
- Classes and Objects
- Constructors and Destructors
- Functions in C + +
- Arrays in C++
- Pointers in C++
- References in C++
- Strings in C++
- Inheritance
- Virtual functions and polymorphism
- Friends in C++
- Operator overloading and type conversions
- Files and Stream
HyperTex Markup Language (HTML)
- Introduction to tree
- Binary tree
- Representing binary trees in memory
Trees
Tree is a non linear data structure. It is used to represent data containing a hierarchical relationship between elements. A binary tree is a special kind of tree. It can be easily maintained in the computer.
Binary trees
A binary tree T is defined as a finite set of elements, called nodes, such that
- T is empty (called the null tree or empty tree) or
- T contains a distinguished node R, called root of T and the remaining nodes of T form an ordered pair of disjoint binary trees T 1 and T 2 .
An Example:
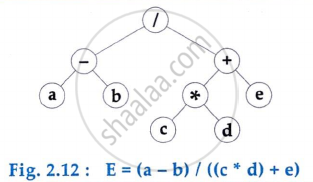
The tree T is said to be complete if all its levels, except the last, have maximum number of possible nodes.
Representing binary trees in memory
Let T be a binary tree. T can be represented in memory either by link representation or by using array called sequential representation.
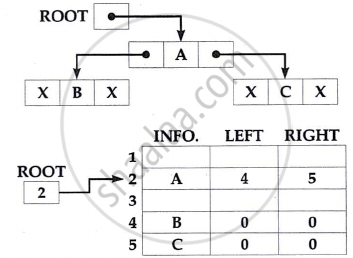
Linked representation
The linked representation uses three parallel arrays, INFO, LEFT and RIGHT and a pointer variable ROOT. Each node N of T will correspond to a location K such that:
- INFO [K] contains the data at node N.
- LEFT [K] contains the location of left child of node N.
- RIGHT [K] contains the location of right child of node N.
Root will contain location of root R of T.
A sample:
Sequential representation:
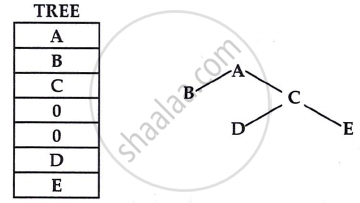
Here a linear array is used. The root R is stored in TREE [1]. If a node N occupies TREE [K], then its left child is stored in TREE [2 * K] and right child in TREE [2 * K + l]. An example is shown in figure: