Question

4 सभी ज्रिज्या का एक वृत्त खोचिए। इसका काई दो जीवाएँ खांचिए। इन दोनों जीवाओं के लंब समद्रिभाजक खींचिए। ये कहाँ मिलते हैं?

Answer 1

1. शीट पर कोई भी बिंदु C अंकित करें। अब परकार को 4 सेमी तक समायोजित करके और परकार के सूचक को बिंदु C पर रखकर, परकार को धीरे-धीरे घुमाकर वृत्त बनाएं। यह 4 सेमी त्रिज्या का अभीष्ट वृत्त है।
   
2. वृत्त में कोई दो जीवाएँ AB और CD लीजिए।
   
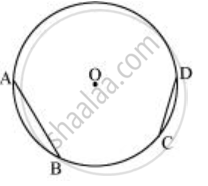
3. A और B को केंद्र मानकर और AB के आधे से अधिक त्रिज्या के साथ, AB के दोनों किनारों पर चाप लगाएँ, जो एक दूसरे को E, F पर काटते हैं। EF को मिलाएँ जो AB का लंबवत समद्विभाजक है।
   
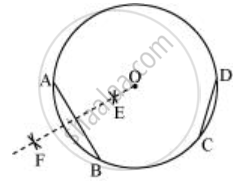
4. C और D को केंद्र मानकर और CD के आधे से अधिक त्रिज्या के साथ, CD के दोनों किनारों पर चाप बनाएं, जो एक दूसरे को G, H पर काटते हैं। GH को मिलाएँ जो CD का लंबवत समद्विभाजक है।
   
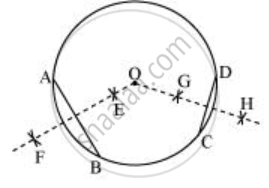
   अब, हम पाएंगे कि जब EF और GH को बढ़ाया जाता है, तो वे वृत्त के केंद्र यानी बिंदु O पर मिलते हैं।