Advertisements
Advertisements
प्रश्न
A(1, −5), B(2, 2) and C(−2, 4) are the vertices of triangle ABC. Find the equation of the median of the triangle through A.
उत्तर
We know the median through A will pass through the mid-point of BC.
Let AD be the median through A.
Co-ordinates of the mid-point of BC, i.e., D are
`((2 - 2)/2, (2 + 4)/2)`
= `(0/2, 6/2)`
= (0, 3)
Slope of AD = `(3 + 5)/(0 - 1) = -8`
Equation of the median AD is
y – 3 = –8(x – 0)
8x + y = 3
APPEARS IN
संबंधित प्रश्न
Find the equation of the line passing through (−5, 7) and parallel to y-axis
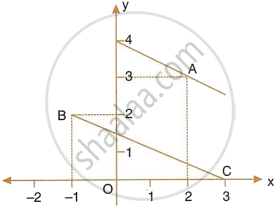
In the following diagram, write down:
- the co-ordinates of the points A, B and C.
- the equation of the line through A and parallel to BC.
Find the value of k such that the line (k – 2)x + (k + 3)y – 5 = 0 is:
- perpendicular to the line 2x – y + 7 = 0
- parallel to it.
ABCD is a parallelogram where A(x, y), B(5, 8), C(4, 7) and D(2, −4). Find:
- co-ordinates of A.
- equation of diagonal BD.
Find the slope of a line perpendicular to the foloowing line 3x - 5y = 9
Find the value of a line perpendicular to the given line x-4y = 8
Find the value of a line perpendicular to the given line 9x-3y = 5
Find the equation of the perpendicular bisector of AB if the coordinates of A and B are (2,6) and ( 4,6).
Find the equation of a line perpendicular to the join of A(3,5) and B(-1,7) if it passes through the midpoint of AB.
Find the equation of a line passing through the intersection of `"x"/10 + "y"/5` = 14 and `"x"/8 + "y"/6` = 15 and perpendicular to the line x - 2y = 5
