Question

A 1 kg block situated on a rough incline is connected to a spring of spring constant 100 N m^–1as shown in Fig. The block is released from rest with the spring in the unstretched position. The block moves 10 cm down the incline before coming to rest. Find the coefficient of friction between the block and the incline. Assume that the spring has a negligible mass and the pulley is frictionless.

Answer 1

Mass of the block, m = 1 kg

Spring constant, k = 100 N m^–1

Displacement in the block, x = 10 cm = 0.1 m

The given situation can be shown as in the following figure.

At equilibrium:

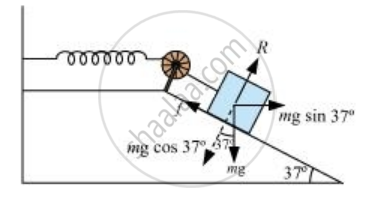
Normal reaction, R = mg cos 37°

Frictional force, f = μ R = mg Sin 37⁰

Where, μ is the coefficient of friction

Net force acting on the block = mg sin37° – f

= mgsin 37° – μmgcos 37°

= mg(sin 37° – μcos 37°)

At equilibrium, the work done by the block is equal to the potential energy of the spring, i.e.,

mg(sin 37° – μcos 37°)x = (1/2)kx²

1 × 9.8 (Sin 37⁰ - μcos 37°) = (1/2) × 100 × (0.1)

0.602 - μ × 0.799 = 0.510

∴ μ = 0.092 / 0.799  =  0.115

Answer 2

From the above figure

`R = mg cos theta`

`F = muR = mu mg cos theta`

Net  Force on the block dpown the incline

`= mg sin theta - F`

`= mg sin theta - mu  mg cos theta`

`= mg(sin theta - mu cos theta)`

Here distance moved x =10 cm = 0.1 m

In equilibrium

work done = Potential enery of stretched spring

`mg(sin theta - mu cos theta) x =  1/2 kx^2`

or `2mg(sin theta - mu  cos theta) = kx`

or `2xx1 kg xx 10ms^(-2)(sin 37^@ - mu cos 37^@) = 100xx 0.1 m`

or `20(0.601 - mu xx 0.798) = 10`

or `0.601 - 0.798mu = 10/20 = 0.5` 

or `-0.798 mu  = 0.5 - 0.601 = -0.101`

or `mu = -0.101/-0.798 = 101/798 = 0.126`

Hence `mu = 0.126`