Advertisements
Advertisements
प्रश्न
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings Specific heat of aluminium = 0.91 J g–1 K–1
Advertisements
उत्तर १
Power of the drilling machine, P = 10 kW = 10 × 103 W
Mass of the aluminum block, m = 8.0 kg = 8 × 103 g
Time for which the machine is used, t = 2.5 min = 2.5 × 60 = 150 s
Specific heat of aluminium, c = 0.91 J g–1 K–1
Rise in the temperature of the block after drilling = δT
Total energy of the drilling machine = Pt
= 10 × 103 × 150
= 1.5 × 106 J
It is given that only 50% of the power is useful.
Useful energy, `triangle Q = 50/100 xx 1.5 xx 10^6 = 7.5xx10^5 J`
But `triangle Q = mctriangle T`
`:. triangle T = (triangle Q)/"mc"`
`= (7.5 xx 10^5)/(8xx10^3xx0.91)`
`= 103 ^@C`
Therefore, in 2.5 minutes of drilling, the rise in the temperature of the block is 103°C.
उत्तर २
Power = 10 kW = 104 W
Mass, m=8.0 kg = 8 x 103 g
Rise in temperature, `triangle T =?`
`Time, t = 2.5 min = 2.5 xx 60 = 150 s`
Specific heat, `C = 0.91 Jg^(-1) K^(-1)`
Total energy = Power x Time = `10^4 xx 150 J`
`=15 xx 10^5 J`
As 50% of energy is lost
∴Thermal energy available
`triangle Q = 1/2 xx 15 xx 10^5 = 7.5 xx 10^5 J`
Since `triangle Q = mctrangle T`
`:.triangle T = triangleQ/mc = (7.5xx20^5)/(8xx10^3xx0.91) = 103^@C`
APPEARS IN
संबंधित प्रश्न
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10–5 K–1.
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1, steel = 1.2 × 10–5 K–1).
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.
A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20°C.
Find the longitudinal strain developed in the rod if the temperature rises to 50°C. Coefficient of linear expansion of steel = 1.2 × 10–5 °C–1.
Show that the moment of inertia of a solid body of any shape changes with temperature as I = I0 (1 + 2αθ), where I0 is the moment of inertia at 0°C and α is the coefficient of linear expansion of the solid.
Answer the following question.
State applications of thermal expansion.
Answer the following question.
What is thermal stress?
A clock pendulum having coefficient of linear expansion. α = 9 × 10-7/°C-1 has a period of 0.5 s at 20°C. If the clock is used in a climate, where the temperature is 30°C, how much time does the clock lose in each oscillation? (g = constant)
A metre scale made of a metal reads accurately at 25 °C. Suppose in an experiment an accuracy of 0.12 mm in 1 m is required, the range of temperature in which the experiment can be performed with this metre scale is ______.(coefficient of linear expansion of the metal is `20 xx 10^-6 / (°"C")`
A metal rod is heated to t°C. A metal rod has length, area of cross-section, Young's modulus and coefficient of linear expansion as 'L', 'A', 'Y' and 'a' respectively. When the rod is heated, the work performed is ______.
A metal rod of cross-sectional area 3 × 10-6 m2 is suspended vertically from one end has a length 0.4 m at 100°C. Now the rod is cooled upto 0°C, but prevented from contracting by attaching a mass 'm' at the lower end. The value of 'm' is ______.
(Y = 1011 N/m2, coefficient of linear expansion = 10-5/K, g = 10m/s2)
The volume of a metal block changes by 0.86% when heated through 200 °C then its coefficient of cubical expansion is ______.
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of 57°C is drunk. You can take body (tooth) temperature to be 37°C and α = 1.7 × 10–5/°C, bulk modulus for copper = 140 × 109 N/m2.
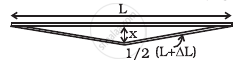
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
- Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
- Reason R: On heating, the length of the rod increases. In light of the above statements.
choose the correct answer from the options given below:
When a solid is heated, its atoms vibrate faster and move farther apart. This happens because ______.
A metallic bar of Young’s modulus, 0.5 × 1011 N m−2 and coefficient of linear thermal expansion 10−5°C−1, length 1 m and area of cross-section 10−3 m2 is heated from 0°C to 100°C without expansion of bending. The compressive force developed in it is ______.
