Advertisements
Advertisements
प्रश्न
A capacitor of capacitance 5⋅00 µF is charged to 24⋅0 V and another capacitor of capacitance 6⋅0 µF is charged to 12⋅0 V. (a) Find the energy stored in each capacitor. (b) The positive plate of the first capacitor is now connected to the negative plate of the second and vice versa. Find the new charges on the capacitors. (c) Find the loss of electrostatic energy during the process. (d) Where does this energy go?
उत्तर
Given :
`C_1 = 5 "uF" and V_1 = 24 V`
`therefore q_1 = C_1V_1 = 5 xx 24 = 120 "uC"`
and
`C_2 = 6 "uF" and V_2 = 12 V`
`therefore q_2 = C_2V_2 = 6 xx 12 = 72 "uC"`
(a)
Energy stored in the first capacitor :
`U_1 = 1/2 C_1V_1^2`
= `1440 "J" = 1.44 "mJ"`
Energy stored in the second capacitor :
`U_2 = 1/2 C_1V_2^2`
= `432 "J" = 0.432 "mJ"`
(b) The capacitors are connected to each other in such a way that the positive plate of the first capacitor is connected to the negative plate of the second capacitor and vice versa.
∴ Net change in the system, `Q_"net" = 120 - 72 = 48`
Now, let V be the common potential of the two capacitors.
From the conservation of charge before and after connecting, we get
`V = Q_"net"/((C_1 + C_2))`
= `48/((5+6))`
= 4.36 V
New charges :
`q_1^' = C_1V = 5 xx 4.36 = 21.8 "uC"`
and
`q_2^' = C_2V = 6 xx 4.36 = 26.2 "uC"`
(c)
Given :
`U_1 = 1/2 C_1V^2`
and
`U_2 = 1/2 C_2V^2`
`therefore U_f = 1/2 V_2 (C_1 + C_2)`
= `1/2 (4.36)^2 (5+6)`
= `1/2 xx 19 xx 11`
= `104.5 xx 10^-6 "J"`
= `0.1045 "mJ"`
`"But" U_i = 1.44 + 0.433 = 1.873`
Loss of Energy :
`ΔU = 1.873 - 0.1045`
= 1.7678
= `1.77 "mJ"`
(d) The energy is dissipated as heat.
APPEARS IN
संबंधित प्रश्न
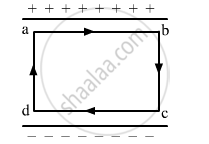
The electric field inside a parallel plate capacitor is E. Find the amount of work done in moving a charge q over a closed loop a b c d a.
Three capacitors of capacitances 2 pF, 3 pF and 4 pF are connected in parallel. Determine the charge on each capacitor if the combination is connected to a 100 V supply.
A cylindrical capacitor has two co-axial cylinders of length 15 cm and radii 1.5 cm and 1.4 cm. The outer cylinder is earthed and the inner cylinder is given a charge of 3.5 µC. Determine the capacitance of the system and the potential of the inner cylinder. Neglect end effects (i.e., bending of field lines at the ends).
Deduce an expression for equivalent capacitance C when three capacitors C1, C2 and C3 connected in parallel.
Figure 4 below shows a capacitor C, an inductor L and a resistor R, connected in series
to an a.c. supply of 220 V

Calculate:
1) The resonant frequency of the given CLR circuit.
2) Current flowing through·the circuit.
3) Average power consumed by the circuit.
A circuit is set up by connecting inductance L = 100 mH, resistor R = 100 Ω and a capacitor of reactance 200 Ω in series. An alternating emf of \[150\sqrt{2}\] V, 500/π Hz is applies across this series combination. Calculate the power dissipated in the resistor.
Suppose a charge +Q1 is given to the positive plate and a charge −Q2 to the negative plate of a capacitor. What is the "charge on the capacitor"?
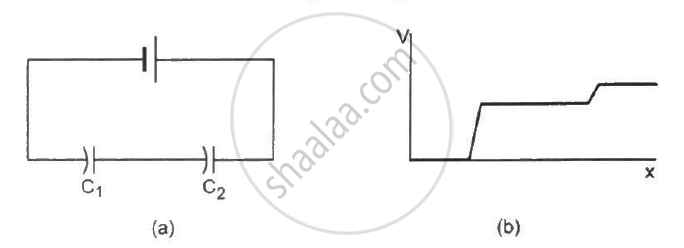
The following figure shows two capacitors connected in series and joined to a battery. The graph shows the variation in potential as one moves from left to right on the branch containing the capacitors.
The separation between the plates of a charged parallel-plate capacitor is increased. Which of the following quantities will change?
(a) Charge on the capacitor
(b) Potential difference across the capacitor
(c) Energy of the capacitor
(d) Energy density between the plates
A parallel-plate capacitor having plate area 25 cm2 and separation 1⋅00 mm is connected to a battery of 6⋅0 V. Calculate the charge flown through the battery. How much work has been done by the battery during the process?
The plates of a capacitor are 2⋅00 cm apart. An electron-proton pair is released somewhere in the gap between the plates and it is found that the proton reaches the negative plate at the same time as the electron reaches the positive plate. At what distance from the negative plate was the pair released?
Three capacitors of capacitance `C_1 = 3muf` , `C_2 = 6muf` , `C_3 = 10muf` , are connected to a 10V battery as shown in figure 3 below :
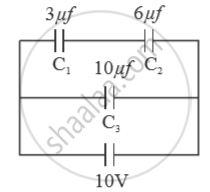
Calculate :
(a) Equivalent capacitance.
(b) Electrostatic potential energy stored in the system
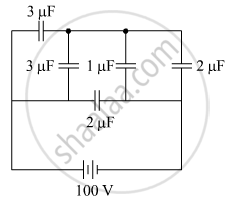
The figure shows a network of five capacitors connected to a 100 V supply. Calculate the total energy stored in the network.
Three capacitors each of 4 µF are to be connected in such a way that the effective capacitance is 6µF. This can be done by connecting them:
Capacitors connected in series have ______
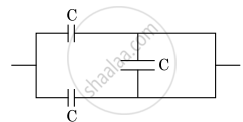
The equivalent capacitance of the combination shown in the figure is ______.
In the circuit shown in figure, initially K1 is closed and K2 is open. What are the charges on each capacitors.
Then K1 was opened and K2 was closed (order is important), What will be the charge on each capacitor now? [C = 1µF]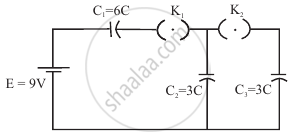
Two equal capacitors are first connected in series and then in parallel The ratio of the equivalent capacities in the two cases will be ______.
The capacitors, each of 4 µF are to be connected in such a way that the effective capacitance of the combination is 6 µF. This can be achieved by connecting ______.
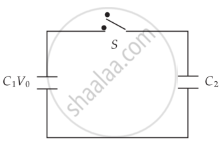
A capacitor of capacity C1 is charged to the potential of V0. On disconnecting with the battery, it is connected with an uncharged capacitor of capacity C2 as shown in the adjoining figure. Find the ratio of energies before and after the connection of switch S.