Advertisements
Advertisements
प्रश्न
A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 360 μC. When potential across the capacitor is reduced by 120 V, the charge stored in it becomes 120 μC.
Calculate:
(i) The potential V and the unknown capacitance C.
(ii) What will be the charge stored in the capacitor, if the voltage applied had increased by 120 V?
उत्तर
(i) Initial voltage, V1 = V volts and charge stored, Q1 = 360 µC.
Q1 = CV1 …(1)
Changed potential, V2 = V − 120
Q2 = 120 µC
Q2 = CV2 ...(2)
By dividing (2) from (1), we get `Q_1/Q_2 = (CV_1)/(CV_1) ⇒360/120 = V/(V-120)⇒ V= 180` volts
`∴C = Q_1/V_1 =( 360 xx10^-6)/180 = 2 xx 10^-6 F = 2μF`
(ii) If the voltage applied had increased by 120 V, then V3 = 180 + 120 = 300 V
Hence, charge stored in the capacitor, Q3 = CV3 = 2×10-6×300 = 600 µC
संबंधित प्रश्न
A capacitor of capacitance C is charged fully by connecting it to a battery of emf E. It is then disconnected from the battery. If the separation between the plates of the capacitor is now doubled, how will the following change?
(i) charge stored by the capacitor.
(ii) Field strength between the plates.
(iii) Energy stored by the capacitor.
Justify your answer in each case.
A capacitor of capacitance ‘C’ is charged to ‘V’ volts by a battery. After some time the battery is disconnected and the distance between the plates is doubled. Now a slab of dielectric constant, 1 < k < 2, is introduced to fill the space between the plates. How will the following be affected? (b) The energy stored in the capacitor Justify your answer by writing the necessary expressions
Three identical capacitors C1, C2 and C3 of capacitance 6 μF each are connected to a 12 V battery as shown.
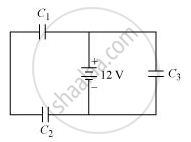
Find
(i) charge on each capacitor
(ii) equivalent capacitance of the network
(iii) energy stored in the network of capacitors
A capacitor of capacitance C is charged to a potential V. The flux of the electric field through a closed surface enclosing the capacitor is
Three capacitors having capacitances 20 µF, 30 µF and 40 µF are connected in series with a 12 V battery. Find the charge on each of the capacitors. How much work has been done by the battery in charging the capacitors?
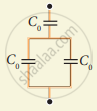
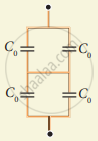
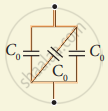
Calculate the resultant capacitances for each of the following combinations of capacitors.
A capacitor is charged by a battery. The battery is removed and another identical uncharged capacitor is connected in parallel. The total electrostatic energy of resulting system ______.
The work done in placing a charge of 8 × 10–18 coulomb on a condenser of capacity 100 micro-farad is ______.
The radius of a sphere of capacity 1 microfarad in the air is ______
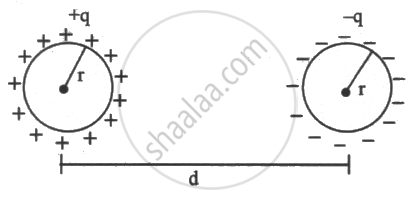
Two similar conducting spheres having charge+ q and -q are placed at 'd' seperation from each other in air. The radius of each ball is r and the separation between their centre is d (d >> r). Calculate the capacitance of the two ball system ______.