Advertisements
Advertisements
प्रश्न
A convex lens of focal length 20 cm is placed coaxially with a concave mirror of focal length 10 cm at a distance of 50 cm apart from each other. A beam of light coming parallel to the principal axis is incident on the convex lens. Find the position of the final image formed by this combination. Draw the ray diagram showing the formation of the image
उत्तर
Let us first locate the image of the point object S formed by the convex lens.
Here:
u = -∞ cm and f = 20 cm
From the lens formula, we have:
`1/v-1/u=1/f`
`=>1/v=1/f+1/u`
`=>1/v=1/20+1/(-oo)`
`=>1/v=1/20`
⇒ v = 20 cm
The positive sign shows that the image is formed to the right of the lens, as shown in the following figure.
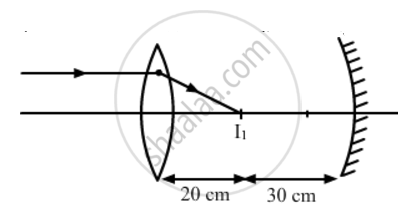
The image I1 is formed in front of the mirror and hence, acts as a real source for the mirror. The concave mirror forms the image I2, whose distance from the mirror can be calculated as:
`1/v=1/u=1/f`
Here:
u=-30 cm ; f=-10 cm
`=>1/v=1/f-1/u`
`=>1/v=-1/10+1/30`
`=>1/v=(1-3)/30=(-2)/30`
⇒ v = − 15 cm
Hence, the final image is formed at a distance of 15 cm from the concave mirror, as shown in the following figure.
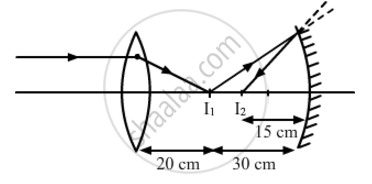
APPEARS IN
संबंधित प्रश्न
An object is placed 15 cm in front of a convex lens of focal length 10 cm. Find the nature and position of the image formed. Where should a concave mirror of radius of curvature 20 cm be placed so that the final image is formed at the position of the object itself?
A convex lens of focal length 20 cm is placed coaxially with a convex mirror of radius of curvature 20 cm. The two are kept 15 cm apart. A point object is placed 40 cm in front of the convex lens. Find the position of the image formed by this combination. Draw the ray diagram showing the image formation.
Draw a ray diagram to show image formation when the concave mirror produces a real, inverted and magnified image of the object.
Use Huygens’ geometrical construction to show the behavior of a plane wavefront.
(i) Passing through a biconvex lens;
(ii) Reflecting by a concave mirror
A particle goes in a circle of radius 2.0 cm. A concave mirror of focal length 20 cm is placed with its principal axis passing through the centre of the circle and perpendicular to its plane. The distance between the pole of the mirror and the centre of the circle is 30 cm. Calculate the radius of the circle formed by the image.
A concave mirror of radius R is kept on a horizontal table (See figure). Water (refractive index = μ) is poured into it up to a height h. Where should an object be placed so that its image is formed on itself?

A particle is moving at a constant speed V from a large distance towards a concave mirror of radius R along its principal axis. Find the speed of the image formed by the mirror as a function of the distance x of the particle from the mirror.
A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t < d/V, (b) at a time t > d/V.
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
In the case of a concave mirror of focal length f , when an object is kept between f and 2 f , show that its image is formed beyond 2 f .
