Advertisements
Advertisements
प्रश्न
A convex lens of focal length 20 cm is placed coaxially with a concave mirror of focal length 10 cm at a distance of 50 cm apart from each other. A beam of light coming parallel to the principal axis is incident on the convex lens. Find the position of the final image formed by this combination. Draw the ray diagram showing the formation of the image
उत्तर
Let us first locate the image of the point object S formed by the convex lens.
Here:
u = -∞ cm and f = 20 cm
From the lens formula, we have:
`1/v-1/u=1/f`
`=>1/v=1/f+1/u`
`=>1/v=1/20+1/(-oo)`
`=>1/v=1/20`
⇒ v = 20 cm
The positive sign shows that the image is formed to the right of the lens, as shown in the following figure.
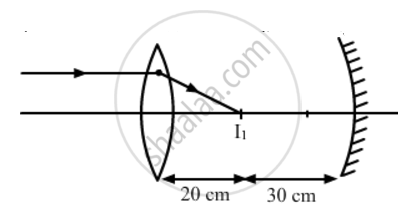
The image I1 is formed in front of the mirror and hence, acts as a real source for the mirror. The concave mirror forms the image I2, whose distance from the mirror can be calculated as:
`1/v=1/u=1/f`
Here:
u=-30 cm ; f=-10 cm
`=>1/v=1/f-1/u`
`=>1/v=-1/10+1/30`
`=>1/v=(1-3)/30=(-2)/30`
⇒ v = − 15 cm
Hence, the final image is formed at a distance of 15 cm from the concave mirror, as shown in the following figure.
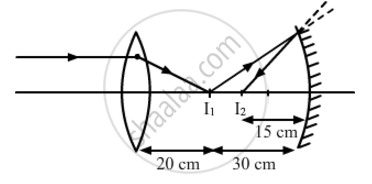
APPEARS IN
संबंधित प्रश्न
Obtain the mirror formula and write the expression for the linear magnification.
A convex lens of focal length 25 cm is placed coaxially in contact with a concave lens of focal length 20 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
A convex lens of focal length 30 cm is placed coaxially in contact with a concave lens of focal length 40 cm. Determine the power of the combination. Will the system be converging or diverging in nature?
An object AB is kept in front of a concave mirror as shown in the figure.
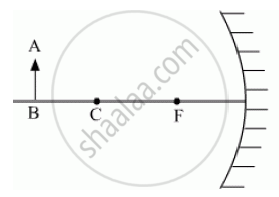
(i) Complete the ray diagram showing the image formation of the object.
(ii) How will the position and intensity of the image be affected if the lower half of the mirror’s reflecting surface is painted black?
Use Huygens’ geometrical construction to show the behavior of a plane wavefront.
(i) Passing through a biconvex lens;
(ii) Reflecting by a concave mirror
Find the diameter of the image of the moon formed by a spherical concave mirror of focal length 7.6 m. The diameter of the moon is 3450 km and the distance between the earth and the moon is 3.8 × 105 km.
A hemispherical portion of the surface of a solid glass sphere (μ = 1.5) of radius r is silvered to make the inner side reflecting. An object is placed on the axis of the hemisphere at a distance 3r from the centre of the sphere. The light from the object is refracted at the unsilvered part, then reflected from the silvered part and again refracted at the unsilvered part. Locate the final image formed.
A small block of mass m and a concave mirror of radius R fitted with a stand lie on a smooth horizontal table with a separation d between them. The mirror together with its stand has a mass m. The block is pushed at t = 0 towards the mirror so that it starts moving towards the mirror at a constant speed V and collides with it. The collision is perfectly elastic. Find the velocity of the image (a) at a time t < d/V, (b) at a time t > d/V.
A gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
Two concave mirrors of equal radii of curvature R are fixed on a stand facing opposite directions. The whole system has a mass m and is kept on a frictionless horizontal table following figure. Two blocks A and B, each of mass m, are placed on the two sides of the stand. At t = 0, the separation between A and the mirrors is 2 R and also the separation between B and the mirrors is 2 R. The block B moves towards the mirror at a speed v. All collisions which take place are elastic. Taking the original position of the mirrors-stand system to be x = 0 and X-axis along AB, find the position of the images of A and B at t = (a) `R/v` (b) `3R/v` (c) `5R/v`.

