Advertisements
Advertisements
प्रश्न
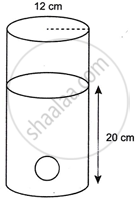
A cylinder of radius 12 cm contains water up to the height 20 cm. A spherical iron ball is dropped into the cylinder and thus water level raised by 6.75 cm. What is the radius of iron ball?
उत्तर
Given:
Radius of cylinder = 12 cm = r1
Water level in cylinder = 20 cm
On dropping sphere ball, rise in height = 6.75 cm = h
Radius of sphere = r2
Now, Volume of water raised in cylinder = Volume of the sphere
⇒ `pir_1^2h = 4/3 pir_2^3`
⇒ `(12 xx 12 xx 6.75) = 4/3 r_2^3`
⇒ r23 = 729
Taking cube root on both sides,
r2 = 9 cm
∴ The radius of the iron ball is 9 cm.
APPEARS IN
संबंधित प्रश्न
Find the diagonal of a square whose side is 10 cm.
The volume of a cube is 1000 cm3. Find the side of a cube.
Find the volume and surface area of a sphere of radius 2.1 cm. `(pi=22/7)`
The sum of length, breadth and height of a cuboid is 38 cm and the length of its diagonal is 22 cm. Find the total surface area of the cuboid.
The volume of a cube is 512 cm3. Find its side.
The radius and slant height of a cone are 5 cm and 20 cm respectively. Find its curved surface area. (Π = 3.14)
If ‘V’ is the volume of a cuboid of dimensions a × b × c and ‘S’ is its surface area, then prove that: `1/V = 2/S[1/a +1/b + 1/c]`
In the given figure, two circles with centres O and P are touching internally at point A. If BQ = 9, DE = 5, complete the following activity to find the radii of the circles.
Find the curved surface area of a sphere of radius 1cm. (π = 3.14)
The dimensions of a cuboid in cm are 30 × 18 × 10. Find its volume.
The volume of a cube is 1000 cm3. Find its total surface area.
Find the volume of a cube with side 6 cm.
The length, breadth, and height of a cuboid are in the ratio 5:4: 2. If the total surface area is 1216 cm2, find dimensions of the solid.
