Advertisements
Advertisements
प्रश्न
A farmer wants to purchase a triangular-shaped land with sides 120 feet and 60 feet and the angle included between these two sides is 60°. If the land costs Rs.500 per square feet, find the amount he needed to purchase the land. Also, find the perimeter of the land
उत्तर
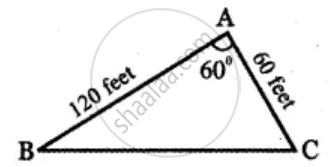
Given AB = 120 ft, AC = 60 ft
∠BAC = 60°
Using cosine formula in ∆ABC
BC2 = AB2 + AC2 – 2AB . AC cos ∠BAC
BC2 = 1202 + 602 – 2 × 120 × 60 cos(60°)
= `144000 + 36000 - 14000 xx 1/2`
= 18000 – 7200
BC2 = 10800 = 100 × 2 × 2 × 3 × 3 × 3
BC2 = 102 × 22 × 32 × 3
BC = `sqrt(10^2 xx 2^2 xx 3^2 xx 3)`
BC = `10 xx 2 xx 3sqrt(3)`
BC = `60sqrt(3)` k.m.
Perimeter of the Land = AB + BC + AC
= `120 + 60sqrt(3) + 60`
= `180 + 60sqrt(3)`
= `60(3 + sqrt(3))` feet.
Area of ∆ABC = `1/2 xx "AB" xx "AC" xx sin∠"BAC"`
= `1/2 xx 60 xx 120 sin 60^circ`
= `30 xx 120 xx sqrt(3)/2`
= `30 xx 60 xx sqrt(3)`
= `1800 sqrt(3)` sq.feet
Cost of 1 sq.feet Rs.500
∴ Cost of `800 sqrt(3)` sq.feet = `800 sqrt(3) xx 500`
= `900000 sqrt(3)`
Total amount needed = `900000 sqrt(3)`
Perimeter of the land = `60(3 + sqrt(3))` feet.
APPEARS IN
संबंधित प्रश्न
Determine whether the following measurements produce one triangle, two triangles or no triangle:
∠B = 88°, a = 23, b = 2. Solve if solution exists
If the sides of a ∆ABC are a = 4, b = 6 and c = 8, then show that 4 cos B + 3 cos C = 2
In a ∆ABC, if a = `sqrt(3) - 1`, b = `sqrt(3) + 1` and C = 60° find the other side and other two angles
In any ∆ABC, prove that the area ∆ = `("b"^2 + "c"^2 - "a"^2)/(4 cot "A")`
In a ∆ABC, if a = 12 cm, b = 8 cm and C = 30°, then show that its area is 24 sq.cm
Two soldiers A and B in two different underground bunkers on a straight road, spot an intruder at the top of a hill. The angle of elevation of the intruder from A and B to the ground level in the eastern direction are 30° and 45° respectively. If A and B stand 5km apart, find the distance of the intruder from B
Two Navy helicopters A and B are flying over the Bay of Bengal at saine altitude from sea level to search a missing boat. Pilots of both the helicopters sight the boat at the same time while they are apart 10 km from each other. If the distance of the boat from A is 6 km and if the line segment AB subtends 60° at the boat, find the distance of the boat from B
A straight tunnel is to be made through a mountain. A surveyor observes the two extremities A and B of the tunnel to be built from a point P in front of the mountain. If AP = 3 km, BP = 5 km, and ∠APB = 120°, then find the length of the tunnel to be built
A plane is 1 km from one landmark and 2 km from another. From the plane’s point of view, the land between them subtends an angle of 45°. How far apart are the landmarks?
A man starts his morning walk at a point A reaches two points B and C and finally back to A such that ∠A = 60° and ∠B = 45°, AC = 4 km in the ∆ABC. Find the total distance he covered during his morning walk
Two vehicles leave the same place P at the same time moving along two different roads. One vehicle moves at an average speed of 60 km/hr and the other vehicle moves at an average speed of 80 km/hr. After half an hour the vehicle reaches destinations A and B. If AB subtends 60° at the initial point P, then find AB
Suppose that a satellite in space, an earth station, and the centre of earth all lie in the same plane. Let r be the radius of earth and R he the distance from the centre of earth to the satellite. Let d be the distance from the earth station to the satellite. Let 30° be the angle of elevation from the earth station to the satellite, If the line segment connecting the earth station and satellite subtends angle α at the centre of earth then prove that d = `"R"sqrt(1 + ("r"/"R")^2 - 2 ("r"/"R") cos alpha)`
Choose the correct alternative:
The triangle of maximum area with constant perimeter 12m
