Advertisements
Advertisements
प्रश्न
A fighter plane flying horizontally at an altitude of 1.5 km with speed 720 km/h passes directly overhead an anti-aircraft gun. At what angle from the vertical should the gun be fired for the shell with muzzle speed 600 m s–1 to hit the plane? At what minimum altitude should the pilot fly the plane to avoid being hit? (Take g = 10 m s–2).
उत्तर १
Height of the fighter plane = 1.5 km = 1500 m
Speed of the fighter plane, v = 720 km/h = 200 m/s
Let θ be the angle with the vertical so that the shell hits the plane. The situation is shown in the given figure.
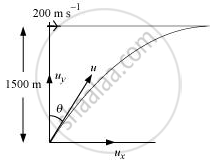
Muzzle velocity of the gun, u = 600 m/s
Time taken by the shell to hit the plane = t
Horizontal distance travelled by the shell = uxt
Distance travelled by the plane = vt
The shell hits the plane. Hence, these two distances must be equal.
uxt = vt
`u sin theta = v`
`sin theta = v/u`
= `200/600 = 1/3 = 0.33`
`theta = sin^(-1)(0.33)`
`= 19.5^@`
In order to avoid being hit by the shell, the pilot must fly the plane at an altitude (H) higher than the maximum height achieved by the shell.
`:.H = (u^2sin^2(90-theta))/"2g"`
`=((600)^2cos^2theta)/(2g)`
`= (360000xxcos^2 19.5)/(2xx10)`
` =18000xx(0.943)^2`
=16006.482 m
=16 km
उत्तर २
Velocity of plane, vp=720 x 5/180 ms-1=200 ms-1
Velocity of shell = 600 `ms^(-1)`
`sin theta = 200/600 = 1/3`
or `theta = sin^(-1)(1/3) = 19.47^@`
This angle is with the verticle.
Let h be the required minimum height
Using equation
`v^2 - u^2 = 2as` we get
`(0)^2-(600 costheta)^2 = -2xx10 xxh`
or `h = (600xx600(1-sin^2theta))/20`
=`30xx600(1-1/9) = 8/9xx30xx600m` = 16 km
APPEARS IN
संबंधित प्रश्न
Rain is falling vertically with a speed of 30 m s–1. A woman rides a bicycle with a speed of 10 m s–1in the north to south direction. What is the direction in which she should hold her umbrella?
A ship A is moving Westwards with a speed of 10 km h–1 and a ship B which is at 100 km South of A, is moving Northwards with a speed of 10 km h–1. The time after which the distance between them becomes shortest, is
Suppose that two objects A and B are moving with velocities `vec("V"_"A")` and `vec("V"_"B")` (each with respect to some common frame of reference). Let `vec("V"_"AB")` represents the velocity of A with respect to B then:
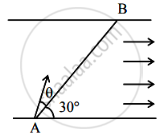
A swimmer wants to cross a river from point A to point B. Line AB makes an angle of 30° with the flow of river. Magnitude of velocity of the swimmer is same as that of the river. The angle θ with the line AB should be ______°, so that the swimmer reaches point B.
A clock has a continuously moving second's hand of 0.1 m length. The average acceleration of the tip of the hand (in units of ms-2) is of the order of ______.
