Advertisements
Advertisements
प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
उत्तर १
No
Range, R = 3 km
Angle of projection, θ = 30°
Acceleration due to gravity, g = 9.8 m/s2
Horizontal range for the projection velocity u0, is given by the relation:
R = `(u^2_0sin2theta)/g`
`3 = u_0^2/g sin 60^@`
`u_0^2/g =2sqrt3` ..(i)
The maximum range (Rmax) is achieved by the bullet when it is fired at an angle of 45° with the horizontal, that is,
`R_"max" = (u_0^2)/g` ..(ii)
On comparing equations (i) and (ii), we get:
`R_"max" = 3sqrt3 = 2 xx 1.732 = 3.46 km`
Hence, the bullet will not hit a target 5 km away
उत्तर २
Here R = 3 km = 3000 m, `theta = 30^@`, g = 9.8 `ms^(-2)`
As R = `(u^2sin 2theta)/g`
`=> 3000 = (u^2sin 2 xx 30^@)/9.8 = (u^2sin 60)/9.8`
`=> u^2 = (3000xx 9.8)/(sqrt3"/2") = 3464 xx 9.8`
Also `R' = (u^2sin 2theta')/g => 5000 = (3464 xx 9.8 xx sin 2theta)/9.8`
i.e `sin 2theta' = 5000/3464 = 1.44`
Which is impossible because sine of an angle cannot be more than 1. Thus this target cannot be hoped to be hit.
APPEARS IN
संबंधित प्रश्न
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
A football is kicked into the air vertically upwards. What is its velocity at the highest point?
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
Two stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angle of projection of one is `pi/3` and its maximum height is y1 then the maximum height of the other will be ______.
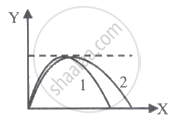
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.
The initial speed of a bullet fired from a rifle is 630 m/s. The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of the target the rifle must be aimed in order to hit the target?
