Advertisements
Advertisements
प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
उत्तर १
No
Range, R = 3 km
Angle of projection, θ = 30°
Acceleration due to gravity, g = 9.8 m/s2
Horizontal range for the projection velocity u0, is given by the relation:
R = `(u^2_0sin2theta)/g`
`3 = u_0^2/g sin 60^@`
`u_0^2/g =2sqrt3` ..(i)
The maximum range (Rmax) is achieved by the bullet when it is fired at an angle of 45° with the horizontal, that is,
`R_"max" = (u_0^2)/g` ..(ii)
On comparing equations (i) and (ii), we get:
`R_"max" = 3sqrt3 = 2 xx 1.732 = 3.46 km`
Hence, the bullet will not hit a target 5 km away
उत्तर २
Here R = 3 km = 3000 m, `theta = 30^@`, g = 9.8 `ms^(-2)`
As R = `(u^2sin 2theta)/g`
`=> 3000 = (u^2sin 2 xx 30^@)/9.8 = (u^2sin 60)/9.8`
`=> u^2 = (3000xx 9.8)/(sqrt3"/2") = 3464 xx 9.8`
Also `R' = (u^2sin 2theta')/g => 5000 = (3464 xx 9.8 xx sin 2theta)/9.8`
i.e `sin 2theta' = 5000/3464 = 1.44`
Which is impossible because sine of an angle cannot be more than 1. Thus this target cannot be hoped to be hit.
APPEARS IN
संबंधित प्रश्न
A man can swim with a speed of 4.0 km/h in still water. How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
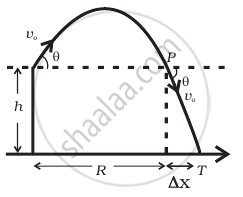
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
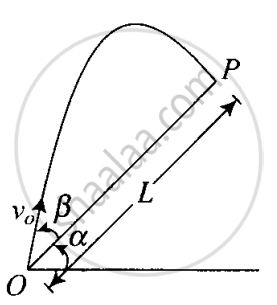
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
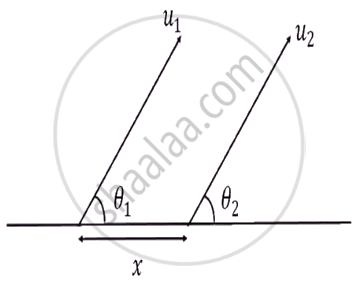
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
A person throws a ball with a speed of 10 m/s at an angle of 30° with horizontally from the top of a 10 m high tower. The distance of the ball from the foot of the tower after falling on the ground will be ______.
