Advertisements
Advertisements
प्रश्न
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
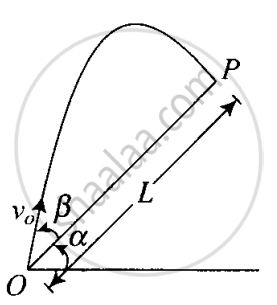
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
उत्तर
a. Since we have, `x = L`
`u_x = v_x = v_0 cos β`
`a_x = - g sin α`
And `t = T = (2v_0 sin β)/(g cos α)`
Hence, `s = u_xt + 1/2 a_xt^2`
Gives us, L = `v_0 cos B * T + 1/2 (- g sin α) T^2`
= `T[v_0 cos β - 1/2 g sin α T]`
Putting `T = (2v_0 sin β)/(g cos α)` given us,
⇒ `L = (2v_0^2 sin β)/(g cos^2 α) cos(α + β)`
That is the required range.
b. Let us first calculate the time of flight.
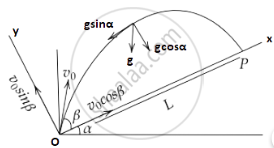
We have,
⇒ `s = ut + 1/2 gt^2`
Where, `s = 0`
`u = u_y = v_0 sin β`
`g = g_y = - g cos α, t = T`
Hence, ⇒ `0 = v_0 sin β (T) + 1/2 (-g cos α)T^2`
i.e. ⇒ `T[v_0 sin β - T g/2 cos α]` = 0
So either T is zero or `v_0 sin β - T g/2 cos α`
That gives the time of flight as `T = (2v_0 sin β)/(g cos α)`
c. Let us consider the equation `Z = sin β cos(α + β)`
We can write `Z = sin β cos(α + β) = 1/2 [sin(2β + α) - sin α]`
Now for Z to be maximum, it must have `sin(2β + α) = 1`
i.e. `sin(2β + α) = sin 90^circ`
That gives, `2β + α = 90^circ`
Hence, `β = (90^circ - α)/2` or `β = pi/4 - α/2`
APPEARS IN
संबंधित प्रश्न
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
A boy throws a ball in air at 60° to the horizontal along a road with a speed of 10 m/s (36 km/h). Another boy sitting in a passing by car observes the ball. Sketch the motion of the ball as observed by the boy in the car, if car has a speed of (18 km/h). Give explanation to support your diagram.
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
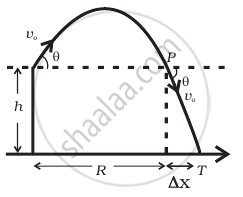
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
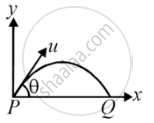
Average torque on a projectile of mass m, initial speed u and angle of projection θ between initial and final positions P and Q as shown in figure about the point of projection is ______.
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
