Advertisements
Advertisements
प्रश्न
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
उत्तर
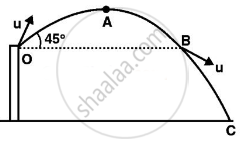
In this problem total mechanical energy of the ball is conserved. As the ball is projected from point O and covers the path OABC.
At point A it has both kinetic and potential energy.
But at point C it has only kinetic energy, (keeping the ground as a reference where PE is zero.)
- At point B, it will gain the same speed as u and after that speed increases and will be maximum just before reaching C.
- During the upward journey from O to A speed decreases and the smallest speed attained by it is at the highest point, i.e., at point A.
- Acceleration is always constant throughout the journey and is vertically downward equal to g.
APPEARS IN
संबंधित प्रश्न
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
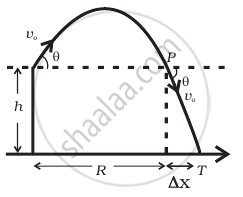
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
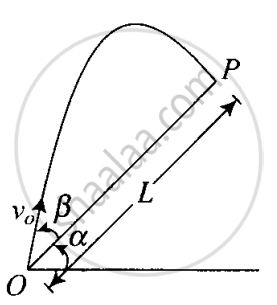
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
If T be the total time of flight of a current of water and H be the maximum height attained by it from the point of projection, then HIT will be : (u = projection velocity, e = projection angle)
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
