Advertisements
Advertisements
प्रश्न
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
उत्तर
Consider the adjacent diagram,
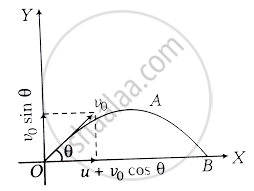
a. Initial velocity in x-direction, `u_x = u + v_0 cos theta`
`u_y` = Initial velocity in y-direction
= `v_0 sin theta`
Where the angle of projection is θ.
Now, we can write
`tan theta = u_y/U_x = (u_0 sin theta)/(u + u_0 cos theta)`
⇒ `θ = tan^-1 ((v_0 sin theta)/(u + v_0 cos theta))`
b. Let T be the time of the flight.
As net displacement is zero over time period T.
`y = 0, u_y = v_0 sin θ, a-y = - g, t = T`
We know that `y = u_yt + 1/2 a_yt^2`
⇒ 0 = `v_0 sin θ T + 1/2 (- g) T^2`
⇒ `T[v_0 sin θ - g/2 T]` = 0
⇒ T = `0, (2v_g sin θ)/g`
T = 01, which corresponds to point O.
Hence, T = `(2u_0 sin θ)/g`
c. Horizontal range, `R(u + v_0 cos θ)`
`T = (u + v_0 cos θ) (2v_0 sin θ)/g`
= `v_0/g [2u sin θ + v_0 sin 2θ]`
d. For horizontal range to be maximum , `(dR)/(dθ)` = 0
⇒ `v_0/g [2u cos θ + v_0 cos 2θ xx 2]` = 0
⇒ `2u cos θ + 2v_0 [2cos^2θ - 1]` = 0
⇒ `4v_0 cos^2θ + 2u cos θ - 2v_0` = 0
⇒ `2v_0 cos^2θ + u cos θ - v_0` = 0
⇒ `cos θ = (-u +- sqrt(u^2 + 8v_0^2))/(4v_0)`
⇒ `θ_"max" cos^-1 [(-u +- sqrt(u^2 + 8v_0^2))/(4v_0)]`
= `cos^-1 [(-u + sqrt(u^2 + 8v_0^2))/(4v_0)]`
e. If u = v0,
`cos θ = (-v_0 +- sqrt(v_0^2 + 8v_0^2))/(4v_0) = (-1 + 3)/4 = 1/2`
If `u < < v_0`, then `8v_0^2 + u^2 ≈ 8v_0^2`
`θ_"max" = cos^-1[(-u +- 2sqrt(2)v_0)/(4v_0)] = cos^-1[1/sqrt(2) - u/(4v_0)]`
If `u < < v_0`, then `θ_"max" = cos^-1 (1/sqrt(2)) = π/4`
If `u > u_0` and `u > > v_0`
`θ_"max" = cos^-1 [(-u +- u)/(4v_0)]` = 0
⇒ `θ_"max" = π/2`
f. If u = 0, `θ_"max" = cos^-1 [(0 +- sqrt(8v_0^2))/(4v_0)]`
= `cos^-1 (1/sqrt(2))`
= 45°
APPEARS IN
संबंधित प्रश्न
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
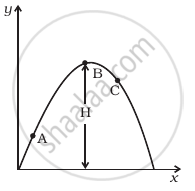
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
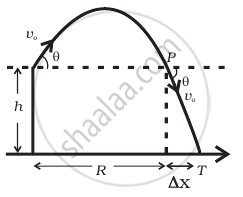
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
A person throws a ball with a speed of 10 m/s at an angle of 30° with horizontally from the top of a 10 m high tower. The distance of the ball from the foot of the tower after falling on the ground will be ______.
