Advertisements
Advertisements
Question
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
Solution
Consider the adjacent diagram,
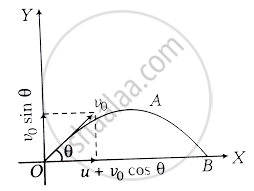
a. Initial velocity in x-direction, `u_x = u + v_0 cos theta`
`u_y` = Initial velocity in y-direction
= `v_0 sin theta`
Where the angle of projection is θ.
Now, we can write
`tan theta = u_y/U_x = (u_0 sin theta)/(u + u_0 cos theta)`
⇒ `θ = tan^-1 ((v_0 sin theta)/(u + v_0 cos theta))`
b. Let T be the time of the flight.
As net displacement is zero over time period T.
`y = 0, u_y = v_0 sin θ, a-y = - g, t = T`
We know that `y = u_yt + 1/2 a_yt^2`
⇒ 0 = `v_0 sin θ T + 1/2 (- g) T^2`
⇒ `T[v_0 sin θ - g/2 T]` = 0
⇒ T = `0, (2v_g sin θ)/g`
T = 01, which corresponds to point O.
Hence, T = `(2u_0 sin θ)/g`
c. Horizontal range, `R(u + v_0 cos θ)`
`T = (u + v_0 cos θ) (2v_0 sin θ)/g`
= `v_0/g [2u sin θ + v_0 sin 2θ]`
d. For horizontal range to be maximum , `(dR)/(dθ)` = 0
⇒ `v_0/g [2u cos θ + v_0 cos 2θ xx 2]` = 0
⇒ `2u cos θ + 2v_0 [2cos^2θ - 1]` = 0
⇒ `4v_0 cos^2θ + 2u cos θ - 2v_0` = 0
⇒ `2v_0 cos^2θ + u cos θ - v_0` = 0
⇒ `cos θ = (-u +- sqrt(u^2 + 8v_0^2))/(4v_0)`
⇒ `θ_"max" cos^-1 [(-u +- sqrt(u^2 + 8v_0^2))/(4v_0)]`
= `cos^-1 [(-u + sqrt(u^2 + 8v_0^2))/(4v_0)]`
e. If u = v0,
`cos θ = (-v_0 +- sqrt(v_0^2 + 8v_0^2))/(4v_0) = (-1 + 3)/4 = 1/2`
If `u < < v_0`, then `8v_0^2 + u^2 ≈ 8v_0^2`
`θ_"max" = cos^-1[(-u +- 2sqrt(2)v_0)/(4v_0)] = cos^-1[1/sqrt(2) - u/(4v_0)]`
If `u < < v_0`, then `θ_"max" = cos^-1 (1/sqrt(2)) = π/4`
If `u > u_0` and `u > > v_0`
`θ_"max" = cos^-1 [(-u +- u)/(4v_0)]` = 0
⇒ `θ_"max" = π/2`
f. If u = 0, `θ_"max" = cos^-1 [(0 +- sqrt(8v_0^2))/(4v_0)]`
= `cos^-1 (1/sqrt(2))`
= 45°
APPEARS IN
RELATED QUESTIONS
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
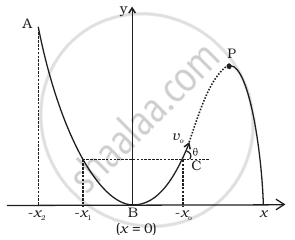
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
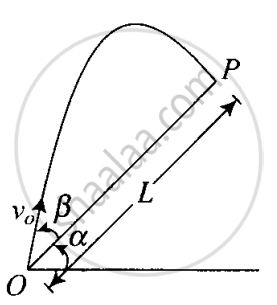
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A girl riding a bicycle with a speed of 5 m/s towards north direction, observes rain falling vertically down. If she increases her speed to 10 m/s, rain appears to meet her at 45° to the vertical. What is the speed of the rain? In what direction does rain fall as observed by a ground based observer?
A circular disc of radius r = 5m is rotating in horizontal plane about y-axis. Y-axis is vertical axis passing through the centre of disc and x-z is the horizontal plane at ground. The height of disc above ground is h = 5 m. Small particles are ejecting from disc in horizontal direction with speed 12 m/s from the circumference of disc then the distance of these particles from origin when they hits the x-z plane is:
Two stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angle of projection of one is `pi/3` and its maximum height is y1 then the maximum height of the other will be ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
