Advertisements
Advertisements
Question
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian co-ordinates A = `A_xhati + A_yhatj` where `hati` and `hatj` are unit vector along x and y directions, respectively and Ax and Ay are corresponding components of (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates as A = `A_rhatr + A_θhatθ` where `hatr = r/r = cos θhati + sin θj` and `hatθ = - sin θhati + cos θ hatj` are unit vectors along direction in which `r` and `θ` are increasing.
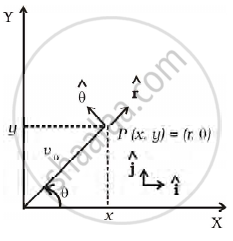
- Express `hati` and `hatj` in terms of `hatr` and `hatθ`
- Show that both `hatr` and `hatθ` are unit vectors and are perpendicular to each other.
- Show that `d/(dt) (hatr) = ωhatθ` where `θ = (dθ)/(dt)` and `d/(dt) (hatθ) = - ωhatr`
- For a particle moving along a spiral given by `t = aθhatr`, where a = 1 (unit), find dimensions of ‘a’.
- Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
Solution
a. Given, unit vetor `hatr = cos θhati + sinθhatj` ......(i)
`hatθ = - sin θ hati + cos θhatj` ......(ii)
Multiplying equation (i) by sin θ and equation (ii) with cos θ and adding
`hatr sin θ + hatθ cos θ = sin θ. cos θhati + sin^2 θhatj + cos^2 θhatj - sinθ. cos θhati`
= `hatj (cos^2 θ + sin^2 θ) = hatj`
⇒ `hatr sin θ + θ cos θ = hatj`
By equation (i) `xx cos θ` - equation (ii) `xx sin θ`
`n(hatr cos θ - hatθ sin θ) = hati`
b. `hatr.hatθ = (cos θhati + sinθhatj) . (- sin θhati + cosθhatj)`
= `- cos θ . sin θ + sin θ . cos θ`
= 0
⇒ θ = 90° Angle between `hatr` and `hatθ`
c. Given, `hatr = cos θhati + sinθhatj`
`(dhatr)/(dt) = d/(dt) (cos θhati + sinθhatj)`
= `- sin θ . (dθ)/(dt) hati + cos θ . (dθ)/(dt) hatj`
= `ω [- sin θhati + cos θhatj]` ......`[∵ θ = (dθ)/(dt)]`
d. Given, `r = aθhatr`, here, writing dimensions `[r] = [a][θ][hatr]`
⇒ L = [a] % 1
⇒ L = [M0L1T0]
e. Given, a = 1 unit `r = θhatr = θ[cos θhati + sin θhatj]`
Velocity, v = `(dr)/(dt) = (dθ)/(dt) hatr + θ d/(dt) hatr = (dθ)/(dt) hatr + θ d/(dt) [(cos θhati + sinθhatj)]`
= `(dθ)/(dt) hatr + θ [(- sin hati + cos θ hatj) (dθ)/(dt)]`
= `(dθ)/(dt) hatr + θ hatθ ω`
= `ωhatr + ω θhatθ`
Acceleration, a = `d/(dt) [ωhatr + ωθhatθ]`
= `d/(dt) [(dθ)/(dt) hatr + (dθ)/(dt) (θhatθ)]`
= `(d^2θ)/(dt^2) hatr + (dθ)/(dt) * (dhatr)/(dt) + (d^2θ)/(dt^2) θhatθ + (dθ)/(dt) d/(dt) (θhatθ)`
= `(d^2θ)/(dt^2) hatr + ω[-sin θhati + sinθhatj] + (d^2θ)/(dt^2) θhatθ + (ωd)/(dt) (θhatθ)`
= `(d^2θ)/(dt^2) hatr + ω^2hatθ + (d^2θ)/(dt^2) xx θhatθ + ω^2hatθ + w^2θ (-hatr) ((d^2θ)/(dtv^2) - ω^2)hatr + (2ω^2 + (d^2θ)/(dt^2) θ)θ`
APPEARS IN
RELATED QUESTIONS
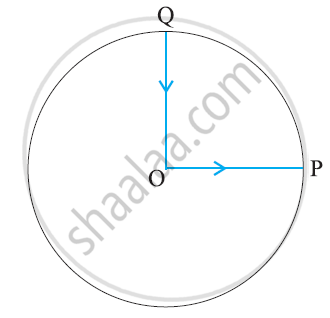
A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in figure. If the round trip takes 10 min, what is the (a) net displacement, (b) average velocity, and (c) average speed of the cyclist?
On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
For any arbitrary motion in space, state whether the following statement is true:
`"a"_"average"=["v"("t"_2) - "v"("t"_1)]/("t"_2 - "t"_1)`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = `(1/2)("v"("t"_1) + "v"("t"_2))`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = [r(t2) - r(t1) ] /(t2 – t1)
For any arbitrary motion in space, state whether the following statement is true:
`"r"("t") = "r"(0) + "v"(0)"t" + 1/2 "a" "t"^2 `
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then, which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
A stone is dropped from the top of the tower and travels 24.5 m in the last second of its journey. The height of the tower is ______.
(g = 9.8 m/s2)
