Advertisements
Advertisements
Question
For any arbitrary motion in space, state whether the following statement is true:
`"r"("t") = "r"(0) + "v"(0)"t" + 1/2 "a" "t"^2 `
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
Options
True
False
Solution
This statement is False.
Explanation:
The particle's motion is arbitrary; the acceleration of the particle may also be non-uniform. Hence, this equation cannot represent the motion of a particle in space.
APPEARS IN
RELATED QUESTIONS
In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?
For any arbitrary motion in space, state whether the following statement is true:
`"a"_"average"=["v"("t"_2) - "v"("t"_1)]/("t"_2 - "t"_1)`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = `(1/2)("v"("t"_1) + "v"("t"_2))`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
v (t) = v (0) + a t
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then, which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian co-ordinates A = `A_xhati + A_yhatj` where `hati` and `hatj` are unit vector along x and y directions, respectively and Ax and Ay are corresponding components of (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates as A = `A_rhatr + A_θhatθ` where `hatr = r/r = cos θhati + sin θj` and `hatθ = - sin θhati + cos θ hatj` are unit vectors along direction in which `r` and `θ` are increasing.
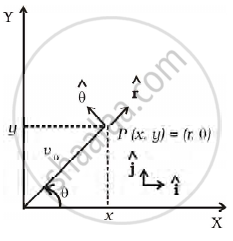
- Express `hati` and `hatj` in terms of `hatr` and `hatθ`
- Show that both `hatr` and `hatθ` are unit vectors and are perpendicular to each other.
- Show that `d/(dt) (hatr) = ωhatθ` where `θ = (dθ)/(dt)` and `d/(dt) (hatθ) = - ωhatr`
- For a particle moving along a spiral given by `t = aθhatr`, where a = 1 (unit), find dimensions of ‘a’.
- Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
Two balls A and B are placed at the top of 180 m tall tower. Ball A is released from the top at t = 0 s. Ball B is thrown vertically down with an initial velocity 'u' at t = 2 s. After a certain time, both balls meet 100 m above the ground. Find the value of 'u' in ms-1. [use g = 10 ms -2]:
The position of a particle is x - y plane is described by the variables x = at3 and y = 2at. Then the acceleration of the particle ______.
A particle of mass 10-2 kg is moving along the positive x-axis under the influence of a force F(x) = `-"K"/(2x)^2` where K = 10-2 Nm2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. The velocity of particle will be ______ m/s, when it reaches x = 0.50 m.
