Advertisements
Advertisements
Question
On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
Solution

(i) The path followed by the motorist will be a closed hexagonal path.
Suppose the motorist starts his journey from the , point O. He takes the turn at the point C.
Displacement = `vec(OC)`
Here OC = `sqrt((OB)^2+(BC)^2) =sqrt((OF+FB)^2+(BC)^2)`
`=sqrt((500 cos30^@ + 500 cos 30^@)^2 + (500)^2)`
`=sqrt((2xx500xxsqrt3/2)^2+(500)^2)`
`=500sqrt4 = 1000 m = 1 km`
Total path length = 500 m + 500 m = 1500 m = 1.5 km
`"Magnitude of displacement"/"Total path length" = 1/1.5 = 2/3 = 0.67`
(ii) After completing six turns, the motorist returns to the starting point, creating a closed hexagonal path.
The displacement is zero since the start and end points coincide |`vec("OC")`| = 0`
The total path length is 6 × 500 = 3,000 metres
Ratio of magnitude of displacement and path length is zero.
(iii) At the eighth turn, the motorist reaches point B. The displacement is the straight-line distance from the starting point O to point B.
Since ∠BOA = ∠OBA = 30°, by trigonometry, the horizontal and vertical components of the displacement are equal to OA cos(30°) and AB cos(30°), respectively.
The total displacement |`vec("OB")`| is twice the horizontal component ON3, because OA = AB, each being 500 m. Thus:
|`vec("OB")`| = 2 × 500 × cos(30°)
= `1000xxsqrt(3)/2 = 500sqrt(3) "m"`
= 0.866 km
The total path length after eight turns is 8 × 500 = 4000 m
`("|"vec("OB")"|")/"Path Length" = (500sqrt(3))/4000`
= `sqrt(3)/8`
APPEARS IN
RELATED QUESTIONS
In a harbour, wind is blowing at the speed of 72 km/h and the flag on the mast of a boat anchored in the harbour flutters along the N-E direction. If the boat starts moving at a speed of 51 km/h to the north, what is the direction of the flag on the mast of the boat?
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = `(1/2)("v"("t"_1) + "v"("t"_2))`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = [r(t2) - r(t1) ] /(t2 – t1)
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian co-ordinates A = `A_xhati + A_yhatj` where `hati` and `hatj` are unit vector along x and y directions, respectively and Ax and Ay are corresponding components of (Figure). Motion can also be studied by expressing vectors in circular polar co-ordinates as A = `A_rhatr + A_θhatθ` where `hatr = r/r = cos θhati + sin θj` and `hatθ = - sin θhati + cos θ hatj` are unit vectors along direction in which `r` and `θ` are increasing.
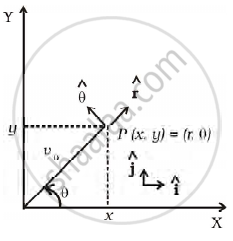
- Express `hati` and `hatj` in terms of `hatr` and `hatθ`
- Show that both `hatr` and `hatθ` are unit vectors and are perpendicular to each other.
- Show that `d/(dt) (hatr) = ωhatθ` where `θ = (dθ)/(dt)` and `d/(dt) (hatθ) = - ωhatr`
- For a particle moving along a spiral given by `t = aθhatr`, where a = 1 (unit), find dimensions of ‘a’.
- Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.
Two balls A and B are placed at the top of 180 m tall tower. Ball A is released from the top at t = 0 s. Ball B is thrown vertically down with an initial velocity 'u' at t = 2 s. After a certain time, both balls meet 100 m above the ground. Find the value of 'u' in ms-1. [use g = 10 ms -2]:
Two vectors `vec"A"` and `vec"B"` have equal magnitudes. If magnitude of `vec"A"` + `vec"B"` is equal to two times the magnitude of `vec"A"` - `vec"B"`, then the angle between `vec"A"` and `vec"B"` will be :
A particle of mass 10-2 kg is moving along the positive x-axis under the influence of a force F(x) = `-"K"/(2x)^2` where K = 10-2 Nm2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. The velocity of particle will be ______ m/s, when it reaches x = 0.50 m.
Boat travels upstream in a river and at t = 0 a wooden cork is thrown over the side with zero initial velocity. After 7.5 minutes the boat turns and starts moving downstream catches the cork when it has drifted 1 km downstream. Then the velocity of water current is ______.
A displacement vector, at an angle of 30° with y-axis has an x-component of 10 units. Then the magnitude of the vector is ______.
The displacement s of a particle depends on time t according to the following relation `s = 1/3t^3 - t^2 + t`. The velocity and displacement of the particle at the instant when its acceleration is zero, are respectively ______.
