Advertisements
Advertisements
प्रश्न
On an open ground, a motorist follows a track that turns to his left by an angle of 60° after every 500 m. Starting from a given turn, specify the displacement of the motorist at the third, sixth and eighth turn. Compare the magnitude of the displacement with the total path length covered by the motorist in each case.
उत्तर

(i) The path followed by the motorist will be a closed hexagonal path.
Suppose the motorist starts his journey from the , point O. He takes the turn at the point C.
Displacement = `vec(OC)`
Here OC = `sqrt((OB)^2+(BC)^2) =sqrt((OF+FB)^2+(BC)^2)`
`=sqrt((500 cos30^@ + 500 cos 30^@)^2 + (500)^2)`
`=sqrt((2xx500xxsqrt3/2)^2+(500)^2)`
`=500sqrt4 = 1000 m = 1 km`
Total path length = 500 m + 500 m = 1500 m = 1.5 km
`"Magnitude of displacement"/"Total path length" = 1/1.5 = 2/3 = 0.67`
(ii) After completing six turns, the motorist returns to the starting point, creating a closed hexagonal path.
The displacement is zero since the start and end points coincide |`vec("OC")`| = 0`
The total path length is 6 × 500 = 3,000 metres
Ratio of magnitude of displacement and path length is zero.
(iii) At the eighth turn, the motorist reaches point B. The displacement is the straight-line distance from the starting point O to point B.
Since ∠BOA = ∠OBA = 30°, by trigonometry, the horizontal and vertical components of the displacement are equal to OA cos(30°) and AB cos(30°), respectively.
The total displacement |`vec("OB")`| is twice the horizontal component ON3, because OA = AB, each being 500 m. Thus:
|`vec("OB")`| = 2 × 500 × cos(30°)
= `1000xxsqrt(3)/2 = 500sqrt(3) "m"`
= 0.866 km
The total path length after eight turns is 8 × 500 = 4000 m
`("|"vec("OB")"|")/"Path Length" = (500sqrt(3))/4000`
= `sqrt(3)/8`
APPEARS IN
संबंधित प्रश्न
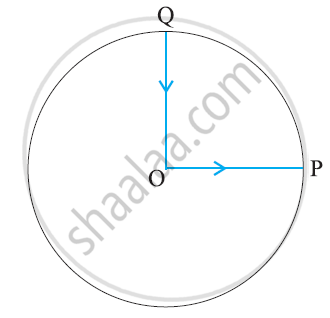
A cyclist starts from the centre O of a circular park of radius 1 km, reaches the edge P of the park, then cycles along the circumference, and returns to the centre along QO as shown in figure. If the round trip takes 10 min, what is the (a) net displacement, (b) average velocity, and (c) average speed of the cyclist?
For any arbitrary motion in space, state whether the following statement is true:
`"V"_"average"` = `(1/2)("v"("t"_1) + "v"("t"_2))`
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
For any arbitrary motion in space, state whether the following statement is true:
`"r"("t") = "r"(0) + "v"(0)"t" + 1/2 "a" "t"^2 `
(The ‘average’ stands for average of the quantity over the time interval t1 to t2)
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then, which of the following are necessarily true?
In a two dimensional motion, instantaneous speed v0 is a positive constant. Then which of the following are necessarily true?
A small toy starts moving from the position of rest under constant acceleration. If it travels a distance of 10 minutes, the distance travelled by the toy in the next will be ______.
The position of a particle is x - y plane is described by the variables x = at3 and y = 2at. Then the acceleration of the particle ______.
A particle of mass 10-2 kg is moving along the positive x-axis under the influence of a force F(x) = `-"K"/(2x)^2` where K = 10-2 Nm2. At time t = 0 it is at x = 1.0 m and its velocity is v = 0. The velocity of particle will be ______ m/s, when it reaches x = 0.50 m.
A displacement vector, at an angle of 30° with y-axis has an x-component of 10 units. Then the magnitude of the vector is ______.
A stone is dropped from the top of the tower and travels 24.5 m in the last second of its journey. The height of the tower is ______.
(g = 9.8 m/s2)
