Advertisements
Advertisements
प्रश्न
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
उत्तर
Consider the adjacent diagram,
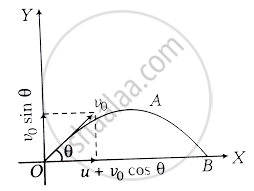
a. Initial velocity in x-direction, `u_x = u + v_0 cos theta`
`u_y` = Initial velocity in y-direction
= `v_0 sin theta`
Where the angle of projection is θ.
Now, we can write
`tan theta = u_y/U_x = (u_0 sin theta)/(u + u_0 cos theta)`
⇒ `θ = tan^-1 ((v_0 sin theta)/(u + v_0 cos theta))`
b. Let T be the time of the flight.
As net displacement is zero over time period T.
`y = 0, u_y = v_0 sin θ, a-y = - g, t = T`
We know that `y = u_yt + 1/2 a_yt^2`
⇒ 0 = `v_0 sin θ T + 1/2 (- g) T^2`
⇒ `T[v_0 sin θ - g/2 T]` = 0
⇒ T = `0, (2v_g sin θ)/g`
T = 01, which corresponds to point O.
Hence, T = `(2u_0 sin θ)/g`
c. Horizontal range, `R(u + v_0 cos θ)`
`T = (u + v_0 cos θ) (2v_0 sin θ)/g`
= `v_0/g [2u sin θ + v_0 sin 2θ]`
d. For horizontal range to be maximum , `(dR)/(dθ)` = 0
⇒ `v_0/g [2u cos θ + v_0 cos 2θ xx 2]` = 0
⇒ `2u cos θ + 2v_0 [2cos^2θ - 1]` = 0
⇒ `4v_0 cos^2θ + 2u cos θ - 2v_0` = 0
⇒ `2v_0 cos^2θ + u cos θ - v_0` = 0
⇒ `cos θ = (-u +- sqrt(u^2 + 8v_0^2))/(4v_0)`
⇒ `θ_"max" cos^-1 [(-u +- sqrt(u^2 + 8v_0^2))/(4v_0)]`
= `cos^-1 [(-u + sqrt(u^2 + 8v_0^2))/(4v_0)]`
e. If u = v0,
`cos θ = (-v_0 +- sqrt(v_0^2 + 8v_0^2))/(4v_0) = (-1 + 3)/4 = 1/2`
If `u < < v_0`, then `8v_0^2 + u^2 ≈ 8v_0^2`
`θ_"max" = cos^-1[(-u +- 2sqrt(2)v_0)/(4v_0)] = cos^-1[1/sqrt(2) - u/(4v_0)]`
If `u < < v_0`, then `θ_"max" = cos^-1 (1/sqrt(2)) = π/4`
If `u > u_0` and `u > > v_0`
`θ_"max" = cos^-1 [(-u +- u)/(4v_0)]` = 0
⇒ `θ_"max" = π/2`
f. If u = 0, `θ_"max" = cos^-1 [(0 +- sqrt(8v_0^2))/(4v_0)]`
= `cos^-1 (1/sqrt(2))`
= 45°
APPEARS IN
संबंधित प्रश्न
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If the second body of mass of 4 m is projected horizontally from the top of a tower of the height of 4 h, it reaches the ground at a distance of 4x from the foot of the tower. The horizontal velocity of the second body is:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
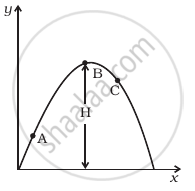
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
A football is kicked into the air vertically upwards. What is its acceleration?
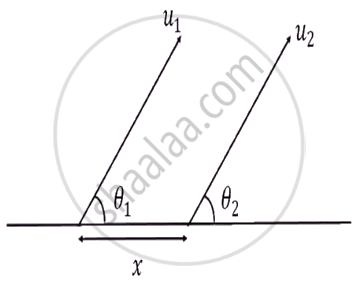
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
A body starts from rest with constant acceleration a, its velocity after n second is v. The displacement of body in last two seconds is ______.
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
A ball is projected from the ground with a speed 15 ms-1 at an angle θ with horizontal so that its range and maximum height are equal, then tan θ will be equal to ______.
