Question

A river is flowing due east with a speed 3 m/s. A swimmer can swim in still water at a speed of 4 m/s (Figure).

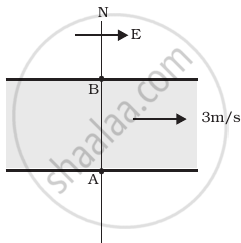
1. If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction)?
2. If he wants to start from point A on south bank and reach opposite point B on north bank, (a) which direction should he swim? (b) what will be his resultant speed?
3. From two different cases as mentioned in (a) and (b) above, in which case will he reach opposite bank in shorter time?

Answer 1

Analysis of Relative Velocity in Different Situations: The motion of a boat (or a swimmer) in running water, say, a river.

a. If the swimmer starts swimming due north, what will be his resultant velocity

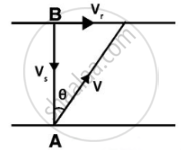
V_s = 4 m/s due north

V_r = 4 m/s due east

Now since both directions are perpendicular,

|Vr|² = 4² + 3² = 5 m/s

`tan θ = V_r/V_s` = 0.75 = 36°54' in the north direction

b. The swimmer wants to start from point A on the south bank and reaches the opposite point B on the north bank

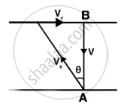
The swimmer makes an angle θ with the north.

From the figure, we have the relation,

`V^2 = v_s^2 = 16 - 9 = 7`

 Hence `v = sqrt(7)` m/s

Now we calculate the value of θ through the below formula,

`tan θ = v_r/v = (3sqrt(7))/7` = 1.13

So, θ = 48°29'30'' in the direction from north to west

c. We need to find from the above two scenarios that for the swimmer to reach the opposite bank in the shorter time

We know that the velocity component perpendicular to the river is 4 m/s

Let us assume the width of the river to be 'w'

Time taken – North

`w/4 = t_1`

Time is taken in part b. when `v = sqrt(7)` m/s

`w/sqrt(7) = t2`

Raking ratio,

`(t_1)/(t_2) = ((w/4))/((w/sqrt(7)))`

`4  t_1 = sqrt(7)  t_2`

Now as , `4 > sqrt(7)`

`t_1 < t_2`

So, the summer will take a shorter time in case a.