Advertisements
Advertisements
Question
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
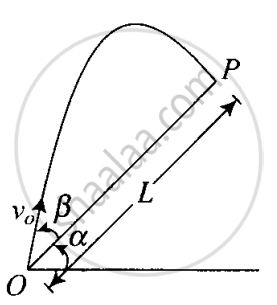
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
Solution
a. Since we have, `x = L`
`u_x = v_x = v_0 cos β`
`a_x = - g sin α`
And `t = T = (2v_0 sin β)/(g cos α)`
Hence, `s = u_xt + 1/2 a_xt^2`
Gives us, L = `v_0 cos B * T + 1/2 (- g sin α) T^2`
= `T[v_0 cos β - 1/2 g sin α T]`
Putting `T = (2v_0 sin β)/(g cos α)` given us,
⇒ `L = (2v_0^2 sin β)/(g cos^2 α) cos(α + β)`
That is the required range.
b. Let us first calculate the time of flight.
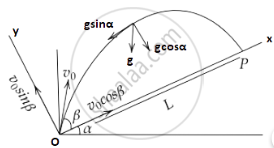
We have,
⇒ `s = ut + 1/2 gt^2`
Where, `s = 0`
`u = u_y = v_0 sin β`
`g = g_y = - g cos α, t = T`
Hence, ⇒ `0 = v_0 sin β (T) + 1/2 (-g cos α)T^2`
i.e. ⇒ `T[v_0 sin β - T g/2 cos α]` = 0
So either T is zero or `v_0 sin β - T g/2 cos α`
That gives the time of flight as `T = (2v_0 sin β)/(g cos α)`
c. Let us consider the equation `Z = sin β cos(α + β)`
We can write `Z = sin β cos(α + β) = 1/2 [sin(2β + α) - sin α]`
Now for Z to be maximum, it must have `sin(2β + α) = 1`
i.e. `sin(2β + α) = sin 90^circ`
That gives, `2β + α = 90^circ`
Hence, `β = (90^circ - α)/2` or `β = pi/4 - α/2`
APPEARS IN
RELATED QUESTIONS
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
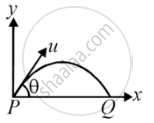
Average torque on a projectile of mass m, initial speed u and angle of projection θ between initial and final positions P and Q as shown in figure about the point of projection is ______.
A body starts from rest with constant acceleration a, its velocity after n second is v. The displacement of body in last two seconds is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
A person throws a ball with a speed of 10 m/s at an angle of 30° with horizontally from the top of a 10 m high tower. The distance of the ball from the foot of the tower after falling on the ground will be ______.
