Question

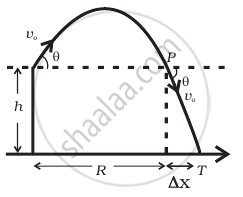
A gun can fire shells with maximum speed v₀ and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`

Answer 1

This problem can be approached in two different ways:

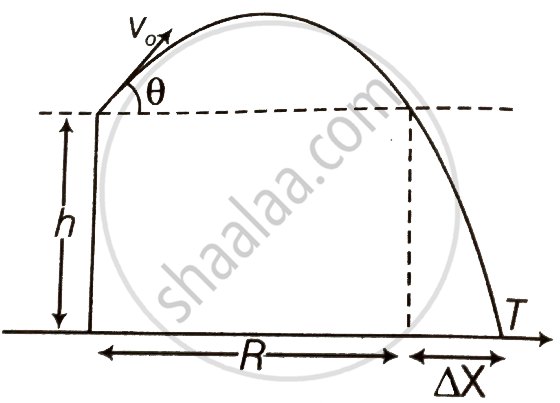
1. Referring to the diagram, target T is at a horizontal distance x = R + Δx and between the point of projection y = – h.
2. From point P in the diagram projection at speed v₀ at an angle θ below horizontal with height h and horizontal range ΔxA)

Applying method (i)

Maximum horizontal range, `R = v_0^2/g`, for θ = 45°  ......(i)

Let the gun be raised through a height h from the ground so that it can hit the target. Let vertically downward direction is taken as positive

The horizontal component of initial velocity = v₀ cos θ

The vertical component of initial velocity = – v₀ sin θ

Taking motion in vertical direction, `h = (- v_0 sin theta) t + 1/2 "gt"^2` ......(ii)

Taking motion in the horizontal direction, `(R + Δx) = v_0 cos θ xx t`

⇒ `t = (R + Δx)/(v_0 cos θ)`  ......(iii)

Substituting the value of t in equation (ii), we get

`h = (- v_0 sin θ) xx ((R + Δx)/(v_0 cos θ)) + 1/2 g ((R + Δx)/(v_0 cos θ))^2`

`h = - (R + Δx) tan θ + 1/2 g  (R + Δx)^2/(v_0^2 cos^2 θ)`

As angle of projection is θ = 45°, therefore

`h = - (R + Δx) + tan 45° + 1/2 g  (R + Δx)^2/(v_0^2 cos^2 45^circ)`

`h = - (R + Δx) xx 1 + 1/2 g  (R + Δx)^2/(v_0^2 (1/2))`  ......`(∵ tan 45^circ = 1 and cos 45^circ = 1/sqrt(2))`

`h = - (R + Δx) + (R + Δx)^2/R`  ......[Using equation (i), R = `"v"_0^2`/g]

= `- (R + Δx) + 1/R (R^2 + Δx^2 + 2RΔx)`

= `- R - Δx + (R + (Δx^2)/R + 2Δx)`

= `Δx + (Δx^2)/R`

`h = Δx(1 + (Δx)/R)` 

Hence proved.