Advertisements
Advertisements
प्रश्न
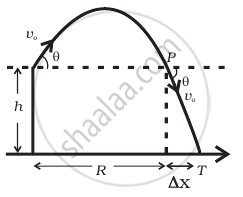
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
उत्तर
This problem can be approached in two different ways:
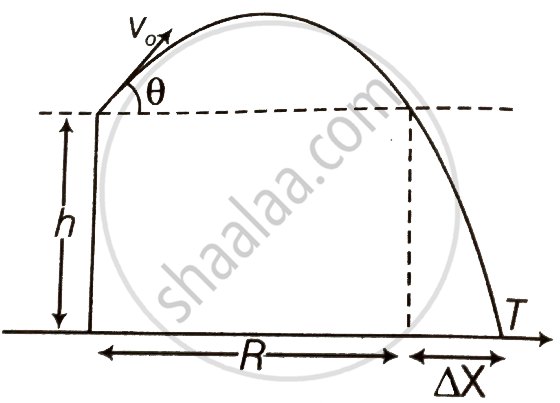
- Referring to the diagram, target T is at a horizontal distance x = R + Δx and between the point of projection y = – h.
- From point P in the diagram projection at speed v0 at an angle θ below horizontal with height h and horizontal range ΔxA)
Applying method (i)
Maximum horizontal range, `R = v_0^2/g`, for θ = 45° ......(i)
Let the gun be raised through a height h from the ground so that it can hit the target. Let vertically downward direction is taken as positive
The horizontal component of initial velocity = v0 cos θ
The vertical component of initial velocity = – v0 sin θ
Taking motion in vertical direction, `h = (- v_0 sin theta) t + 1/2 "gt"^2` ......(ii)
Taking motion in the horizontal direction, `(R + Δx) = v_0 cos θ xx t`
⇒ `t = (R + Δx)/(v_0 cos θ)` ......(iii)
Substituting the value of t in equation (ii), we get
`h = (- v_0 sin θ) xx ((R + Δx)/(v_0 cos θ)) + 1/2 g ((R + Δx)/(v_0 cos θ))^2`
`h = - (R + Δx) tan θ + 1/2 g (R + Δx)^2/(v_0^2 cos^2 θ)`
As angle of projection is θ = 45°, therefore
`h = - (R + Δx) + tan 45° + 1/2 g (R + Δx)^2/(v_0^2 cos^2 45^circ)`
`h = - (R + Δx) xx 1 + 1/2 g (R + Δx)^2/(v_0^2 (1/2))` ......`(∵ tan 45^circ = 1 and cos 45^circ = 1/sqrt(2))`
`h = - (R + Δx) + (R + Δx)^2/R` ......[Using equation (i), R = `"v"_0^2`/g]
= `- (R + Δx) + 1/R (R^2 + Δx^2 + 2RΔx)`
= `- R - Δx + (R + (Δx^2)/R + 2Δx)`
= `Δx + (Δx^2)/R`
`h = Δx(1 + (Δx)/R)`
Hence proved.
APPEARS IN
संबंधित प्रश्न
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If the second body of mass of 4 m is projected horizontally from the top of a tower of the height of 4 h, it reaches the ground at a distance of 4x from the foot of the tower. The horizontal velocity of the second body is:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.