Advertisements
Advertisements
प्रश्न
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
उत्तर
Speed of the ball, u = 40 m/s
Maximum height, h = 25 m
In projectile motion, the maximum height reached by a body projected at an angle θ, is given by the relation:
h = `(u^2sin^2theta)/(2g)`
25 = `((40)^2sin^2theta)/(2xx9.8)`
sin2 θ = 0.30625
sin θ = 0.5534
∴θ = sin–1(0.5534) = 33.60°
Horizontal range, R = `(u^2sin 2theta)/g`
= `((40)^2xxsin2xx33.60) /9.8`
= `(1600xxsin 67.2)/9.8`
= `(1600xx0.922)/9.8 = 150.53 "m"`
APPEARS IN
संबंधित प्रश्न
A man can swim with a speed of 4.0 km/h in still water. How long does he take to cross a river 1.0 km wide if the river flows steadily at 3.0 km/h and he makes his strokes normal to the river current? How far down the river does he go when he reaches the other bank?
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
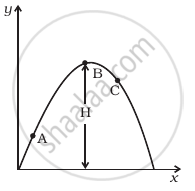
A boy travelling in an open car moving on a levelled road with constant speed tosses a ball vertically up in the air and catches it back. Sketch the motion of the ball as observed by a boy standing on the footpath. Give explanation to support your diagram.
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
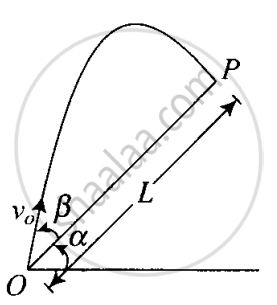
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
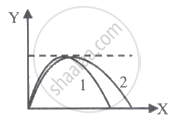
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.
The initial speed of a bullet fired from a rifle is 630 m/s. The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of the target the rifle must be aimed in order to hit the target?
