Advertisements
Advertisements
प्रश्न
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?
उत्तर
Maximum horizontal distance, R = 100 m
The cricketer will only be able to throw the ball to the maximum horizontal distance when the angle of projection is 45°, i.e., θ = 45°.
The horizontal range for a projection velocity v, is given by the relation:
`R = (v^2sin2theta)/g`
`100 = v^2/g sin 90^@`
`v^2/g = 100` ..(i)
The ball will achieve the maximum height when it is thrown vertically upward. For such motion, the final velocity v is zero at the maximum height H.
Acceleration, a = –g
Using the third equation of motion
`v^2 - u^2 = 2gH`
= `(0)^2 - (sqrt(100)g)^2 = 2(-g)H`
`H=(100g)/(2g)=50 "m"`
APPEARS IN
संबंधित प्रश्न
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
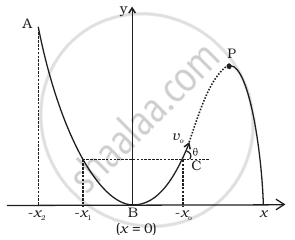
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
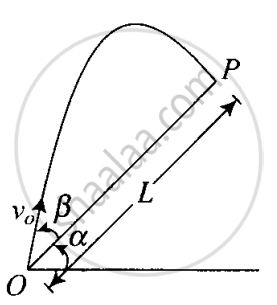
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
If T be the total time of flight of a current of water and H be the maximum height attained by it from the point of projection, then HIT will be : (u = projection velocity, e = projection angle)
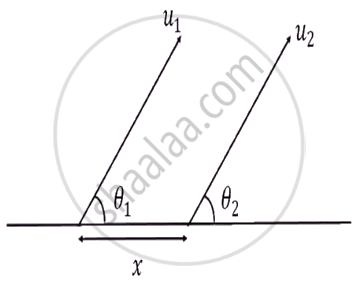
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
A person throws a ball with a speed of 10 m/s at an angle of 30° with horizontally from the top of a 10 m high tower. The distance of the ball from the foot of the tower after falling on the ground will be ______.
