Advertisements
Advertisements
प्रश्न
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
उत्तर
The velocity of the fighter plane at a height h = 1.5 km = 1500 m is given as u = 720 km/h = `720 * 5/18` = 200 m/s
Let the plane drops the bomb t seconds before the target is exactly below the plane.
Then in t seconds, the bomb must cover the vertical distance of 1500 m under free fall with an initial velocity of zero.
Hence, h = `ut + 1/2 gt^2`
That gives, `1500 = 0 + 1/2 10t^2`
`t = sqrt(300) = 10sqrt(3) s`
Now distance covered by the plane is `ut = 200 xx 10sqrt(3) = 2000sqrt(3)`
Hence, `tan theta = 1500/(2000sqrt(3)) = sqrt(3)/4`
Therefore, `θ = tan^-1 sqrt(3)/4` = 23°42'
APPEARS IN
संबंधित प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A body of mass m is projected horizontally with a velocity v from the top of a tower of height h and it reaches the ground at a distance x from the foot of the tower. If the second body of mass of 4 m is projected horizontally from the top of a tower of the height of 4 h, it reaches the ground at a distance of 4x from the foot of the tower. The horizontal velocity of the second body is:
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
The horizontal range of a projectile fired at an angle of 15° is 50 m. If it is fired with the same speed at an angle of 45°, its range will be ______.
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
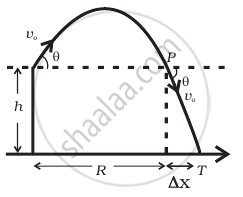
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
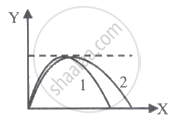
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
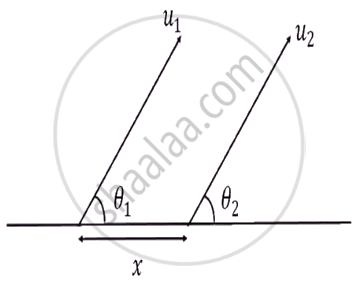
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.
The initial speed of a bullet fired from a rifle is 630 m/s. The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of the target the rifle must be aimed in order to hit the target?
