Advertisements
Advertisements
प्रश्न
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
उत्तर १
Maximum vertical height `h_m = (v_o^2 sin^2theta)/2g` ...(i)
Horiaontal range `R = (v_o^2 sin 2theta)/g` .. (ii)
Solving equations (i) and (ii), we get:
`h_m/R = (sin^2 theta)/(2sin 2theta) = (sin^2theta)/(4sin theta cos theta) = sin theta/(4cos theta)`
`=>h_m/R = (Tan theta)/4`
`=> theta = Tan^(-1) ((4h_m)/R)`
उत्तर २
Since h_"max" = `(u^2sin^2theta)"/2g"`
and `R = (u^2sin 2theta)/g`
`=> h_"max"/R = (u^2sin^2theta"/2g")/(u^2sin 2theta"/g") = (tan theta)/4`
`=> (tan theta)/4 = h_"max"/R`
or `tan theta = (4h_"max")/R`
or `theta = tan^(-1)(4h_"max")/R`

APPEARS IN
संबंधित प्रश्न
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
A cricketer can throw a ball to a maximum horizontal distance of 100 m. How much high above the ground can the cricketer throw the same ball?
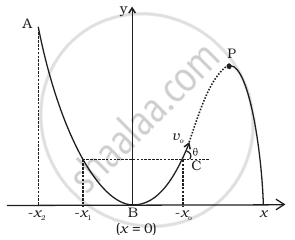
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
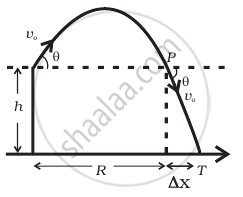
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
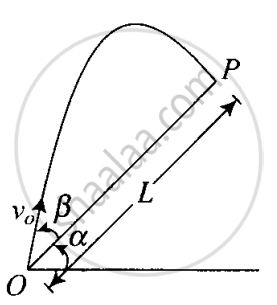
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
If T be the total time of flight of a current of water and H be the maximum height attained by it from the point of projection, then HIT will be : (u = projection velocity, e = projection angle)
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.
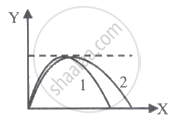
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
