Advertisements
Advertisements
प्रश्न
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
उत्तर १
Let `v_(ox)` and `v_(oy)` respectively be the initial components of the velocity of the projectile along horizontal (x) and vertical (y) directions.
Let `v_x` and `v_y` respectively be the horizontal and vertical components of velocity at a point P.
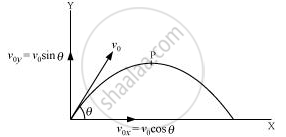
Time taken by the projectile to reach point P = t
Applying the first equation of motion along the vertical and horizontal directions, we get:
`v_y = v_(oy) = "gt"`
And `v_x =v_(ox)`
`:. tan theta = v_y/v_x= (v_(oy) - "gt")/v_(ox)`
`theta = tan^(-1)((v_(oy) - "gt")/(v_(o x)))`
उत्तर २
Let the projectile be fired at an angle `theta` with x-axis.
As `theta` depend on t, `theta(t)` at any instance
`tan theta(t) = v_y/v_x =(v_(oy) - "gt")/(v_(o x))`
(Since `v_y = v_(oy) - "gt" and v_x = v_(o x)`)
`=> theta(t) = tan^(-1)((v_o - "gt")/v_(o x))`
APPEARS IN
संबंधित प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
An aircraft is flying at a height of 3400 m above the ground. If the angle subtended at a ground observation point by the aircraft positions 10.0 s a part is 30°, what is the speed of the aircraft?
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
Two particles are projected in air with speed vo at angles θ1 and θ2 (both acute) to the horizontal, respectively. If the height reached by the first particle is greater than that of the second, then tick the right choices
- Angle of projection: q1 > q2
- Time of flight: T1 > T2
- Horizontal range: R1 > R2
- Total energy: U1 > U2
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
If T be the total time of flight of a current of water and H be the maximum height attained by it from the point of projection, then HIT will be : (u = projection velocity, e = projection angle)
A circular disc of radius r = 5m is rotating in horizontal plane about y-axis. Y-axis is vertical axis passing through the centre of disc and x-z is the horizontal plane at ground. The height of disc above ground is h = 5 m. Small particles are ejecting from disc in horizontal direction with speed 12 m/s from the circumference of disc then the distance of these particles from origin when they hits the x-z plane is:
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
