Advertisements
Advertisements
Question
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
Solution 1
Let `v_(ox)` and `v_(oy)` respectively be the initial components of the velocity of the projectile along horizontal (x) and vertical (y) directions.
Let `v_x` and `v_y` respectively be the horizontal and vertical components of velocity at a point P.
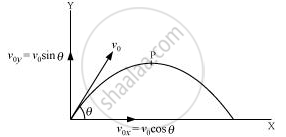
Time taken by the projectile to reach point P = t
Applying the first equation of motion along the vertical and horizontal directions, we get:
`v_y = v_(oy) = "gt"`
And `v_x =v_(ox)`
`:. tan theta = v_y/v_x= (v_(oy) - "gt")/v_(ox)`
`theta = tan^(-1)((v_(oy) - "gt")/(v_(o x)))`
Solution 2
Let the projectile be fired at an angle `theta` with x-axis.
As `theta` depend on t, `theta(t)` at any instance
`tan theta(t) = v_y/v_x =(v_(oy) - "gt")/(v_(o x))`
(Since `v_y = v_(oy) - "gt" and v_x = v_(o x)`)
`=> theta(t) = tan^(-1)((v_o - "gt")/v_(o x))`
APPEARS IN
RELATED QUESTIONS
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A particle moving in a circle of radius R with a uniform speed takes a time T to complete one revolution.
If this particle were projected with the same speed at an angle ‘θ’ to the horizontal, the maximum height attained by it equals 4R. The angle of projection, θ, is then given by ______.
A football is kicked into the air vertically upwards. What is its acceleration?
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
A football is kicked into the air vertically upwards. What is its velocity at the highest point?
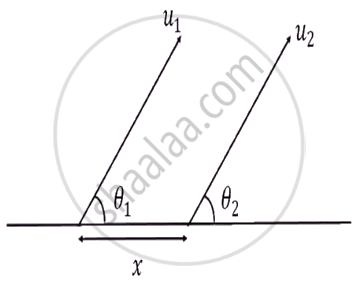
Two particles are projected simultaneously from the level ground as shown in figure. They may collide after a time:
If a baseball player can throw a ball at maximum distance = d over a ground, the maximum vertical height to which he can throw it, will be (Ball has same initial speed in each case):
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
