Advertisements
Advertisements
प्रश्न
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
उत्तर १
Let `v_(ox)` and `v_(oy)` respectively be the initial components of the velocity of the projectile along horizontal (x) and vertical (y) directions.
Let `v_x` and `v_y` respectively be the horizontal and vertical components of velocity at a point P.
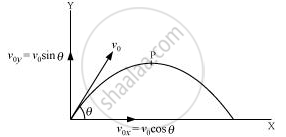
Time taken by the projectile to reach point P = t
Applying the first equation of motion along the vertical and horizontal directions, we get:
`v_y = v_(oy) = "gt"`
And `v_x =v_(ox)`
`:. tan theta = v_y/v_x= (v_(oy) - "gt")/v_(ox)`
`theta = tan^(-1)((v_(oy) - "gt")/(v_(o x)))`
उत्तर २
Let the projectile be fired at an angle `theta` with x-axis.
As `theta` depend on t, `theta(t)` at any instance
`tan theta(t) = v_y/v_x =(v_(oy) - "gt")/(v_(o x))`
(Since `v_y = v_(oy) - "gt" and v_x = v_(o x)`)
`=> theta(t) = tan^(-1)((v_o - "gt")/v_(o x))`
APPEARS IN
संबंधित प्रश्न
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A ball is thrown from a roof top at an angle of 45° above the horizontal. It hits the ground a few seconds later. At what point during its motion, does the ball have
- greatest speed.
- smallest speed.
- greatest acceleration?
Explain
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
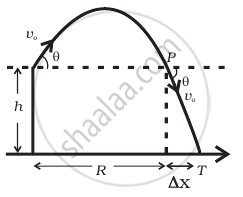
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
A ball is projected from the ground with a speed 15 ms-1 at an angle θ with horizontal so that its range and maximum height are equal, then tan θ will be equal to ______.
The initial speed of a bullet fired from a rifle is 630 m/s. The rifle is fired at the centre of a target 700 m away at the same level as the target. How far above the centre of the target the rifle must be aimed in order to hit the target?
