Advertisements
Advertisements
प्रश्न
A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Advertisements
उत्तर १
0.86 m/s2; 54.46° with the direction of velocity
Speed of the cyclist, v = 27 km/h = 7.5 m/s
Radius of the circular turn, r = 80 m
Centripetal acceleration is given as:
`a_c = v^2/r`
=(7.5)^2/80 = 0.7 `"m/s"^2`
The situation is shown in the given figure:
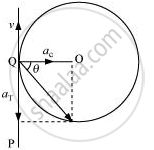
Suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the breaks and decelerates the speed of the bicycle by 0.5 m/s2.
This acceleration is along the tangent at Q and opposite to the direction of motion of the cyclist.
Since the angle between`a_c` and `a_T`is 90°, the resultant acceleration a is given by:
a = `sqrt(a_c^2 + a_T^2)`
=`sqrt((0.7)^2 + (0.5)^2)`
=`sqrt(0.74) = 0.86` `"m/s"^2`
`tan theta = a_c/a_T`
Where `theta` is the angle of the resultant with the direction of velocity
`tan theta = 0.7/0.5 = 1.4`
`theta = tan^(-1)(1.4)`
`=54.46^@`
उत्तर २
Here v = 27 km/h = `27xx5/18` m/s = 7.5 m/s, r = 80 m
and tangential acceleration `a_t = -0.50 "m/s"^2`
:.Centripetal acceleration `a_c = v^2/r = (7.5)^2/80 ms^2` (radially inwards)
Thus as shown in figure two accelerations are mutually perpendicular directions. If `veca` be the resultant acceleration then
|veca| = sqrt(a_t^2+a_c^2) = sqrt((0.5)^2+(0.7)^2) = 0.86 `ms^(-2)`
and tan beta = `a_c/a_t = 0.7/0.5 = 1.4`
`=> beta = tan^(-1) (1.4) = 54.5^@` fromthe direction of negative of the velocity
संबंधित प्रश्न
In U. C. M (Uniform Circular Motion), prove the relation `vec v = vec w xx vec r`, where symbols have their usual meanings.
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.
Explain the meaning of uniform circular motion. Give one example of such motion.
Differentiate between uniform linear motion and uniform circular motion.
A piece of stone tied at the end of a thread is whirled in a horizontal circle with uniform speed by hand. Answer the following questions:
- Is the velocity of stone uniform or variable?
- Is the acceleration of stone uniform or variable?
- What is the direction of acceleration of stone at any instant?
- Which force provides the centripetal force required for circular motion?
- Name the force and its direction which acts on the hand.
The motion of the moon around the earth in a circular path is an accelerated motion.
Which of the following quantity remains constant in a uniform circular motion?
Solve the following problem.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
Which of the following graph represents uniform motion of a moving particle?
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
A string of length 'l' fixed at one end carries a mass 'm' at the other end. The string makes `3/pi` revolutions/second around the vertical axis through the fixed end as shown in figure. The tension 'T' in the string is ______.
A mass 'm' is tied to one end of a spring and whirled in a horizontal circle with constant angular velocity. The elongation in the spring is 1 cm. If the angular speed is doubled, the elongation in the spring is 6 cm. The original length of the spring is ______.
A body moves in a uniform circular motion ______.
Define uniform circular motion and give an example of it. Why is it called accelerated motion?
If a body is moving in a circle of radius r with a constant speed v, its angular velocity is ______.
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
A ceiling fan rotates about its own axis with some angular velocity. When the fan is switched off the angular velocity becomes `(1/4)^"th"` of the original in time 't' and 'n' revolutions are made in that time. The number of revolutions made by the fan during the time interval between switch off and rest are ______. (Angular retardation is uniform)
What is the direction of the velocity of an object at any point during uniform circular motion?
By applying Kepler's third law to the formula for centripetal force, Newton concluded that the force acting on a planet is:
