Advertisements
Advertisements
Question
A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Advertisements
Solution 1
0.86 m/s2; 54.46° with the direction of velocity
Speed of the cyclist, v = 27 km/h = 7.5 m/s
Radius of the circular turn, r = 80 m
Centripetal acceleration is given as:
`a_c = v^2/r`
=(7.5)^2/80 = 0.7 `"m/s"^2`
The situation is shown in the given figure:
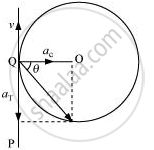
Suppose the cyclist begins cycling from point P and moves toward point Q. At point Q, he applies the breaks and decelerates the speed of the bicycle by 0.5 m/s2.
This acceleration is along the tangent at Q and opposite to the direction of motion of the cyclist.
Since the angle between`a_c` and `a_T`is 90°, the resultant acceleration a is given by:
a = `sqrt(a_c^2 + a_T^2)`
=`sqrt((0.7)^2 + (0.5)^2)`
=`sqrt(0.74) = 0.86` `"m/s"^2`
`tan theta = a_c/a_T`
Where `theta` is the angle of the resultant with the direction of velocity
`tan theta = 0.7/0.5 = 1.4`
`theta = tan^(-1)(1.4)`
`=54.46^@`
Solution 2
Here v = 27 km/h = `27xx5/18` m/s = 7.5 m/s, r = 80 m
and tangential acceleration `a_t = -0.50 "m/s"^2`
:.Centripetal acceleration `a_c = v^2/r = (7.5)^2/80 ms^2` (radially inwards)
Thus as shown in figure two accelerations are mutually perpendicular directions. If `veca` be the resultant acceleration then
|veca| = sqrt(a_t^2+a_c^2) = sqrt((0.5)^2+(0.7)^2) = 0.86 `ms^(-2)`
and tan beta = `a_c/a_t = 0.7/0.5 = 1.4`
`=> beta = tan^(-1) (1.4) = 54.5^@` fromthe direction of negative of the velocity
RELATED QUESTIONS
A particle starts from the origin at t = 0 s with a velocity of 10.0 `hatj "m/s"` and moves in the x-y plane with a constant acceleration of `(8.0 hati + 2.0 hatj) ms^(-2)`.
- At what time is the x-coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?
- What is the speed of the particle at the time?
A vehicle is moving on a circular track whose surface is inclined towards the horizon at an angle of 10°. The maximum velocity with which it can move safely is 36 km / hr. Calculate the length of the circular track. [π = 3.142]
A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
Which of the following quantity remains constant in a uniform circular motion?
Answer the following question.
Show that the centripetal force on a particle undergoing uniform circular motion is -mrω2.
Is the uniform circular motion accelerated? Give reasons for your answer.
The ratio of the angular speed of minute hand and hour hand of a watch is ____________.
A particle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, the radial force acting on the particle is ______.
A wheel is 0.25 m in radius. When it makes 15 revolutions per minute, its linear speed at the point on circumference is ____________.
A particle is perfonning uniform circular motion. If 'θ', 'ω', 'α' and ' a' are its angular displacement, angular velocity, angular acceleration, and centripetal acceleration respectively, then which of the following is 'WRONG'?
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
The angular speed of the minute hand of a clock in degrees per second is ______.
Which of the following is correct about uniform circular motion
- the direction of motion is continuously changed
- the direction of motion is not changed
- speed and direction both remain constant
- speed is constant but the direction is changing
The motion of the bus is ______ motion.
Define uniform circular motion and give an example of it. Why is it called accelerated motion?
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
A particle is given an initial speed u inside a smooth spherical shell of radius R = 1 m that it is just able to complete the circle. Acceleration of the particle when its velocity is vertical is ______.
A simple pendulum of length l has maximum angular displacement θ. The maximum kinetic energy of the bob of mass m is ______.
(g = acceleration due to gravity)
A horizontal circular platform of mass M is rotating at angular velocity ω about a vertical axis passing through its centre. A boy of mass m is standing at the edge of the platform. If the boy comes to the centre of the platform, then the new angular velocity becomes ______.
