Uniform circular motion refers to the circular motion if the magnitude of the velocity of the particle in circular motion remains constant. The non-uniform circular motion refers to the circular motion when the magnitude of the velocity of the object is not constant.
| Uniform Circular Motion | Circular Motion (Non-Uniform) |
|---|---|
| The tip of a clock’s hand | A car turning around a curved track |
| A stone tied to a string and spun in a circle (constant speed) | A roller coaster on a circular loop |
| A point on the rim of a bicycle wheel (at constant speed) | A satellite orbiting the Earth (if speed or path varies) |
| A satellite orbiting the Earth (in circular orbit, constant speed) | A stone tied to a string and spun in a circle (if speed changes) |
Changes in direction
As you increase the number of sides, the number of direction changes increases. If the sides become infinite, the shape becomes a circle, where the direction changes continuously.
This shows that in a circular path, the change in velocity happens only because the direction changes, even if the speed is constant. This type of motion is called uniform circular motion. If an object moves along a circular path with radius 'r' and takes time 't' to return to its starting position, we can determine its speed using the following formula:
Speed = `"Circumference"/"Time"`
v = `"2 πr"/"t"` r = radius of the circle
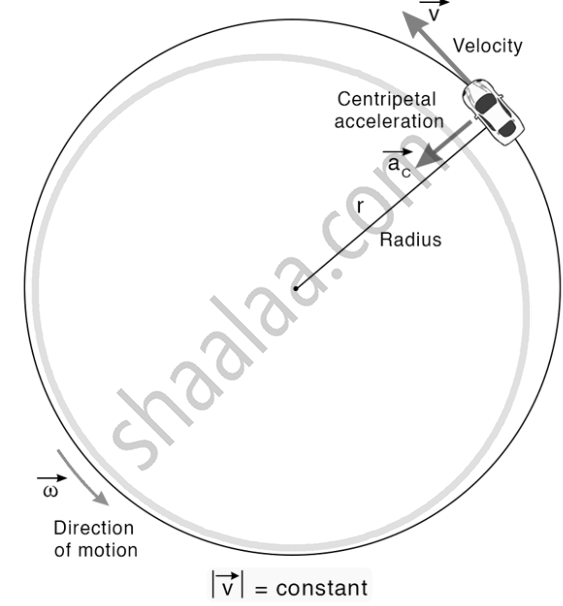
When an object moves in a circular path at a constant speed, its motion is called uniform circular motion and it requires a continuous force directed towards the centre of the circle. This force is called centripetal force.
If is the mass of the object, is its speed, and is the radius of the circle, then it can be shown that this force is equal to:
`(F) = (mv^2)/(r)`
If a planet is revolving around the Sun in a circular orbit in uniform circular motion, then the centripetal force acting on the planet towards the Sun must be:
`(F) = (mv^2)/(r)`
where is the mass of the planet, is its speed, and is its distance from the Sun.
`"Speed " = "distance travelled"/"time taken"`
The speed of the planet can be expressed in terms of the period of revolution as follows:
`"v"="distance travelled"/"time taken"`= \[\frac{2\pi\mathrm{r}}{\Gamma}\]
\[\mathrm{F=\frac{mv^{2}}{r}}\quad=\quad\frac{m\left(\frac{2\pi r}{T}\right)^{2}}{r}\quad=\quad\frac{4m\pi^{2}r}{T^{2}},\mathrm{multiplying~and~dividing~by~r^{2}~we~get},\]
\[\mathrm{F}=\frac{4\mathrm{m}\pi^2}{\mathrm{r}^2}\times\left(\frac{\mathrm{r}^3}{\mathrm{T}^2}\right)\]
According to Kepler’s third law, \[\frac{\mathrm{T}^{2}}{\mathrm{r}^{3}}=\mathrm{K}\]
\[\mathrm{F=~\frac{4~m~\pi^2}{r^2K}~,~But~\frac{4~m~\pi^2}{K}=Constant~\therefore~F=constant\times\frac{1}{r^2}~\therefore~F~\alpha~\frac{1}{r^2}}\]
Thus, Newton concluded that the centripetal force, which is the force acting on the planet and is responsible for its circular motion, must be inversely proportional to the square of the distance between the planet and the Sun.
Newton identified this force with the force of gravity and hence postulated the inverse square law of gravitation. The gravitational force is much weaker than other forces in nature, but it controls the universe and determines its future. This is possible because of the huge masses of planets, stars, and other constituents of the universe.
1. Aim: To study the direction of the velocity of an object moving in a circular path.
2. Requirements: a circular disc, a five-rupee coin, and a pin to fix the disc.
3. Procedure
The coin and the disc
4. Conclusion: The coin is thrown off in the direction of the tangent at the point of release, which is always perpendicular to the radius at that point. This demonstrates that the direction of motion of an object in uniform circular motion is constantly changing along the tangent to the circular path.
1. Angular Displacement (Δθ)
The angle subtended by the position vector at the centre of the circular path is called angular displacement.
`Δθ = (ΔS)/(r)`
where:
Unit: Radian (rad)
2. Angular Acceleration (α)
The rate of change of angular velocity over time.
`α = (dω)/dt` = `(d^2θ) / (dt^2)`
where:
Unit: Radian per second squared (rad/s²)
Dimensional Formula: [T⁻²]
Relation with Linear Acceleration: a = rα
where:
3. Angular Velocity (ω)
The rate of change of angular displacement over time.
`ω = (Δθ)/(Δt)`
where: ν = Linear velocity
4. Centripetal Acceleration (aₙ or ac)
The acceleration acting on a body in circular motion is always directed towards the centre of the circular path.
\[a_c=\frac{v^2}{r}=r\omega^2\]
where:
Also called radial acceleration (as it acts along the radius).
Vector Quantity: It has both magnitude and direction (towards the centre).
Unit: Meter per second squared (m/s²)
