Applications of Bernoulli’s Equation

Bernoulli’s Principle

For a streamlined fluid flow, the sum of the pressure (P), the kinetic energy per unit volume `((ρv)^2/2)` and the potential energy per unit volume (ρgh) remain constant.

Mathematically:- `"P"+ (ρv^2)/2 + ρgh = "constant"`

• where P= pressure,

• `"E"/ ("Volume")=1/2"mv"^2/V = 1/2v2(m/V) = 1/2ρv2`

• `"E"/("Volume") = "mgh"/"V" = ("m"/"V")"gh" = "ρgh"'`

Derive: Bernoulli’s equation:

Mathematically:-

Consider the fluid initially lying between B and D. In an infinitesimal time interval `Delta"t"`, this fluid would have moved.

Suppose `v_1`= speed at B and `v_2`= speed at D, initial distance moved by fluid from B to `"C" = "v"_1Delta"t" `

in the same interval `Delta"t"`fluid distance moved by D to `E = v_2Deltat.`

P1 = pressure A1, P2 = pressure at A2

work done on the fluid at left end(BC) `"W"_1 = "P"_1"A"_1("v"_1Delta"t")`

work done by the fluid at the other end (DE)`"W"_2="P"_2"A"_2("v"_2Delta"t")`

Net work done on the fluid is `"W"_1 -"W"_2=("P"_1"A"_1"v"_1Delta"t"-"P"_2"A"_2"v"_2Delta"t")`

By the equation of contunity Av = constant

`"P"_1"A"_1"v"_1Delta"t"-"P"_2"A"_2"v"_2Delta"t"` where `"A"_1"v"_1Delta"t"="P"_1Delta"V" and "A"_2"v"_2Delta"t" = "P"_2Delta"V"`

Therefore work done = `("P"_1-"P"_2)  Delta"Vequation"("a")`

Part of this work goes in changing kinetic energy, `Delta"K"=1/2"m"("v"_2^2-"v"_1^2)` and part in gravitational potential energy, `Delta"U"="mg"("h"_2-"h"_1)`

The total change in energy `Delta"E" = Delta"K" + Delta"U"=1/2"m"("v"_2^2-"v"_1^2)+"mg"("h"_2-"h"_1)`    ...(i)

Density of fluid `rho="m"/"V" or "m"=rho"V"`

Therefore in small interval of time `Delta"t"`,small change in mass `Delta"m"`.    `Delta"m"=rhoDelta"V"`          ...(ii)

Substituting eq(ii) in eq(i)

`Delta"E"=1/2rhoDelta"V"("v"_2^2-"v"_1^2)+rho"g"Delta"V"("h"_2-"h"_1)`      ....(b)

By using work energy theorem: `"W" = Delta"E"`

From (a) and (b)`

`("P"_1-"P"_2)Delta"V"=1/2rhoDelta"V"("v"_2^2-"v"_1^2)+rhoDelta"V"("h"_2-"h"_1)`

`"P"_1"P"_2 = 1/2rhov_2^2-1/2rhov_1^2+rho"gh"_2-rho"gh"_1`    ...(By cancelling `Delta"V"` from both the sides)

After rearranging we get `P_1+1/2rho"v"_1^2 + rho"gh"_1 = 1/2rho"v"_2^2 + rho"gh"_2`

`"P" + 1/2rho"v"^2+rho"gh"="constant"`

This is the bernoullis equation.

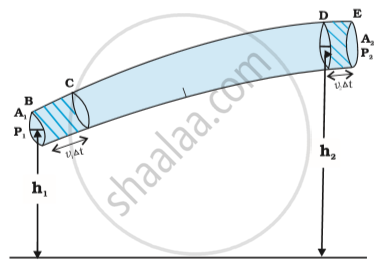
The flow of an ideal fluid in a pipe of varying cross-section. The fluid in a section of length `"v"_1`Δt moves to the section of length `"v"2`Δt in time Δt. 

Special case:

When a fluid is at rest. this means `v_1=v_2=0`

from Bernoulli's equation `P_1+1/2rho"v"_1^2 + rho"gh"_1 = 1/2rho"v"_2^2 + rho"gh"_2`

By putting `v_1=v_2=0` in the above eq.

`"P"_1"P"_2=rho"g"("h"_2-"h"_1)` this eq is same as when the fluids are at rest.

when the pipe is horizontal `h_1=h_2` this means there is no potential energy by the virtue of height.

Therefore from Bernoullis equation `(P_1+1/2rhov_1^2+rhogh_1 = 1/2rhov_2^2+rhogh_2)`

By simplifying, `"P"+1/2rhov^2="constant"`

Torricelli’s law

• Torricelli law states that the speed of flow of fluid from an orifice is equal to the speed that it would attain if falling freely for a distance equal to the height of the free surface of the liquid above the orifice.

• Consider any vessel which has an orifice (slit)filled with some fluid.

• The fluid will start flowing through the slit and according to Torricelli law, the speed with which the fluid will flow is equal to the speed with which a freely falling body attains such that the height from which the body falls is equal to the height of the slit from the free surface of the fluid.

• Let the distance between the free surface and the slit = h

• The velocity with which the fluid flows is equal to the velocity with which a freely falling body attains if it is falling from a height h.

Derivation:

• Let A₁= area of the slit (it is very small), v₁= Velocity with which fluid is flowing out.
• A₂=Area of the free surface of the fluid,v₂=velocity of the fluid at the free surface.
• From Equation of Continuity, Av=constant.Therefore A₁v₁ = A₂v₂.
• From the figure, A₂>>>A₁, This implies v₂<<v₁(This means fluid is at rest on the free surface), Therefore v₂~ 0.
• Using Bernoulli’s equation

`"P" + 1/2rho"v"^2+rho"gh"="constant"`

Applying Bernoulli’s equation at the slit:

`"P"_"a"+1/2rho"v"_1^2+rho"gy"_1`     ...(1)  

where `"P"_a = "Atmospheric pressure", "y"_1="height of the slit from the base".`

applying Bernoullis equation at the surface:

`P+rhogy_2`     ...(2)

where as `v_2=0 therefore1/2rhov_1^2=0,y_2="height of the free surface from the base"`

by equation (1) & (2)

`"P"_a + 1/2rho"v"_1^2 + rho"gy"_1 = "P"+rho"gy"_2`

`1/2rhov_1^2=(P-P_a) + rhog(y_2-y_1)`

`=(P-P_a)rhogh("where h"=(y_2-y_1))`

`v_1^2=2/rho[(P-P_a)+rhogh]`

Therefore `v_1=sqrt2/rho[(P-P_a)+rhogh]` this is the velocity by which the fluid will come out of the small slit.

`v_1`is known as speed of Efflux. this means the speed of the fluid outflow.

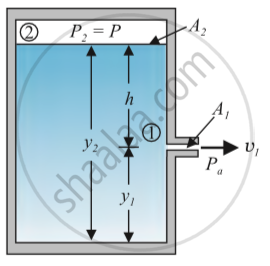
Torricelli’s law:- The speed of efflux, v₁, from the side of the container is given by the application of Bernoulli’s equation.

Case1:- The vessel is not closed it is open to the atmosphere that means P=Pa.

• Therefore `"v"_1=sqrt(2"gh")`.This is the speed of a freely falling body.

• This is in accordance with Torricelli’s law which states that the speed by which the fluid is flowing out of a small slit of a container is the same as the velocity of a freely falling body.

• Case2:-Tank is not open to the atmosphere but P>>P_a.

• Therefore 2gh is ignored as it is very very large, hence `"v"_1=sqrt(2"p")/rho`

• The velocity with which the fluid will come out of the container is determined by the pressure at the free surface of the fluid alone.

Problem: -Calculate the velocity of the emergence of a liquid from a hole in the side of a wide cell 15cm below the liquid surface?

Answer:-

By using Torricelli’s law `"v"_1=sqrt(2"gh")`

`=2xx9.8xx15xx10^-2"m"//"s"`

=1.7m/s

Venturimeter

• Venturimeter is a device to measure the flow of incompressible liquid.

• It consists of a tube with a broad diameter having a larger cross-sectional area but there is a small constriction in the middle.

• It is attached to the U-tube manometer. One end of the manometer is connected to the constriction and the other end is connected to the broader end of the Venturimeter.

• The U-tube is filled with a fluid whose density is ρ.

• `"A"_1`= cross-sectional area at the broader end, `"v"_1` = velocity of the fluid.

• `"A"_2`=cross-sectional area at the constriction, `"v"2`= velocity of the fluid.

• By the equation of continuity, wherever the area is more velocity is less and vice-versa. As `"A"_1` is more this implies `"v"_1` is less and vice-versa.

• The pressure is inversely ∝ to Therefore at `"A"_1` pressure `"P"_1` is less as compared to pressure `"P"_2` at `"A"_2`.

• This implies `"P"_1<"P"_2` as `"v"_1>"v"_2`.

• As there is a difference in the pressure the fluid moves, this movement of the fluid is marked by the level of the fluid increase at one end of the U-tube.

Venturimeter: determining the fluid speed.

By equation of continuity:- `"A"_1"v"_1="A"_2"v"_2`

This implies `"v"_2=("A"_1/"A"_2)"V"_1`     ...(1)

By bernoullis equation:-

`"P"_1+1/2rho"v"_1^2 + rho"gh"_1 = 1/2rho"v"_2^2 + rho"gh"_2`

As height is the same we can ignore the term `rhog`

This implies `P_1-P_2=1/2rho(v_2^2-v_1^2)`

`=1/2rho(A_1^2/A_2^2(v_1^2-v_1^2))`

`=1/2rho(A_1^2/A_2^2-1)`

As there is pressure difference the level of the fluid in the U-tube changes.

`("P"_1-"P"_2)=hrho_mg   "where"  rho_m` (density of the fluid inside the manometer).

`1/2rho"v"_1^2("A"_1^2/"A"_2^2-1)="h"rho_m"g"` 

`v_1=2"h"rho_m"g"/rho["A"_1^2/"A"_2^2-1]^-(1/2)`

Practical Application of Venturimeter:

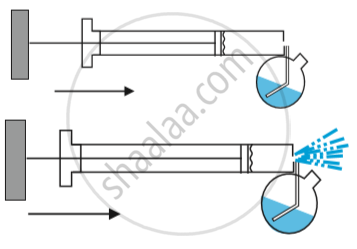
1. Spray Gun or perfume bottle- They are based on the principle of Venturimeter.

• Consider a bottle filled with fluid which has a pipe that goes straight till constriction. There is a narrow end of a pipe that has a greater cross-sectional area.

• The cross-sectional area of constriction which is in the middle is less.

• There is pressure difference when we spray as a result some air goes in, the velocity of the air changes depending on the cross-sectional area.

• Also because of the difference in the cross-sectional area there is a pressure difference, the level of the fluid rises and it comes out.

• Dynamic Lift

• Dynamic lift is the normal force that acts on a body by virtue of its motion through a fluid.

• Consider an object which is moving through the fluid, and due to the motion of the object through the fluid, there is a normal force that acts on the body.

• This force is known as dynamic lift.

• Dynamic lift is most popularly observed in airplanes.

• Whenever an aeroplane is flying in the air, due to its motion through the fluid here fluid is air in the atmosphere. Due to its motion through this fluid, there is a normal force that acts on the body in the vertically upward direction.

• This force is known as Dynamic lift.

• Examples:

• Airplane wings

• Spinning ball in the air

Dynamic lift on airplane wings:-

• Consider an aeroplane whose body is streamlined. Below the wings of the aeroplane there is air that exerts an upward force on the wings. As a result, aeroplane experiences a dynamic lift.

Magnus Effect

• Dynamic lift by virtue of spinning is known as the Magnus effect.

• Magnus effect is a special name given to dynamic lift by virtue of spinning.

• Example:-Spinning of a ball.

Case1:-When the ball is not spinning.

• The ball moves in the air it does not spin, the velocity of the ball above and below the ball is the same.

• As a result, there is no pressure difference.(ΔP= 0).

• Therefore there is no dynamic lift.

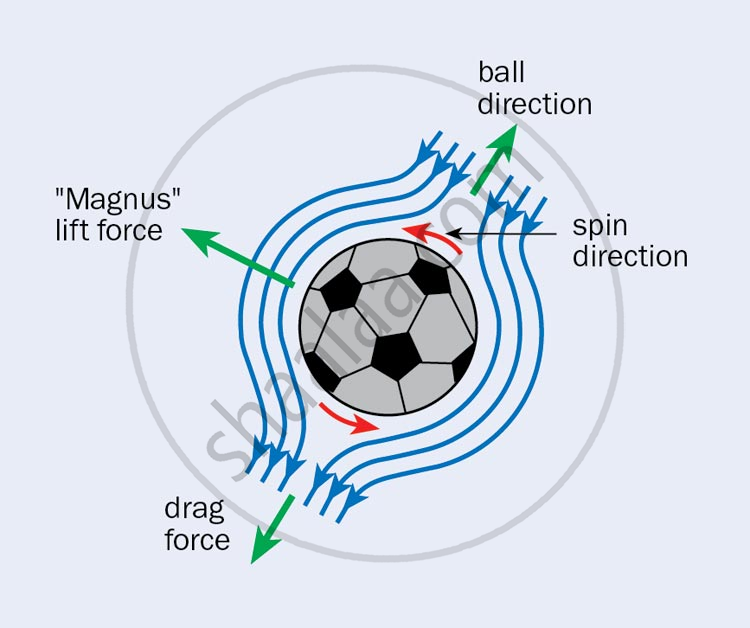
Case2:- When the ball is moving in the air as well as spinning.

• When the ball spins it drags the air above it, therefore, the velocity above the ball is more as compared to the velocity below the ball.

• As a result, there is a pressure difference; the pressure is more below the ball.

• Because of the pressure difference, there is an upward force which is the dynamic lift.

Problem:- A fully loaded Boeing aircraft has a mass of 3.3x10⁵kg. Its total wing area is 500m². It is a level flight with a speed of 960km/h. Estimate the pressure difference between the lower and upper surfaces of the wings.

Answer:-

Weight of the aircraft= Dynamic lift

`"mg" = ("P"_1-"P"_2)"A"`

`"mg"/"A"=DeltaP`

`DeltaP=3.3xx10^5xx9.8/500`

=6.5x10³ N/m²