Question

A point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = `Ksqrt(S)` where 'K' is a constant. If 'e' is the angle between the total acceleration and tangential acceleration, then

Options

• tan θ = `sqrt(S/R)`

• tan θ = `sqrt(S/(2R))`

• tan θ = `S/(2R)`

• tan θ = `(2S)/R`

Answer 1

tan θ = `(2S)/R`

Explanation:

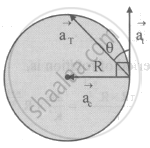
The object's velocity is reported as

V = `Ksqrt(S)`  ......(i)

The object's centripetal acceleration is,

a_c = `V^2/R`  .....(ii)

Tangential acceleration is represented by,

a_t = `(dV)/(dt) = (dV)/(dS) (dS)/(dt)`

= `V (dV)/(dS)`

= `Ksqrt(S) d/(dS) (Ksqrt(S))`  .......[From (i)]

= `K^2 sqrt(S) 1/(2sqrt(S))`

a_t = `K^2/2`  .......(iii)

From figure,

tan θ = `a_c/a_t = (V^2/R) 2/K^2`  .....[From (ii) and (iii)]

∴ tan θ = `2/R (K^2S)/K^2`

∴ tan θ = `(2S)/R`