Advertisements
Advertisements
Question
The ceiling of a long hall is 25 m high. What is the maximum horizontal distance that a ball thrown with a speed of 40 m s–1 can go without hitting the ceiling of the hall?
Solution
Speed of the ball, u = 40 m/s
Maximum height, h = 25 m
In projectile motion, the maximum height reached by a body projected at an angle θ, is given by the relation:
h = `(u^2sin^2theta)/(2g)`
25 = `((40)^2sin^2theta)/(2xx9.8)`
sin2 θ = 0.30625
sin θ = 0.5534
∴θ = sin–1(0.5534) = 33.60°
Horizontal range, R = `(u^2sin 2theta)/g`
= `((40)^2xxsin2xx33.60) /9.8`
= `(1600xxsin 67.2)/9.8`
= `(1600xx0.922)/9.8 = 150.53 "m"`
APPEARS IN
RELATED QUESTIONS
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
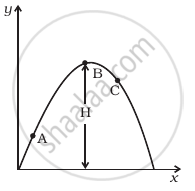
A football is kicked into the air vertically upwards. What is its acceleration?
A fighter plane is flying horizontally at an altitude of 1.5 km with speed 720 km/h. At what angle of sight (w.r.t. horizontal) when the target is seen, should the pilot drop the bomb in order to attack the target?
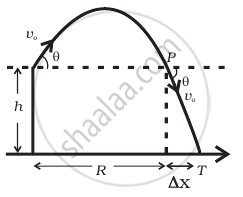
A gun can fire shells with maximum speed v0 and the maximum horizontal range that can be achieved is R = `v_0^2/g`. If a target farther away by distance ∆x (beyond R) has to be hit with the same gun (Figure), show that it could be achieved by raising the gun to a height at least `h = Δx[ 1 + (Δx)/R]`
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
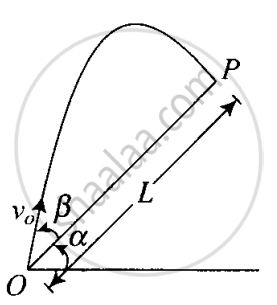
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
