Advertisements
Advertisements
Question
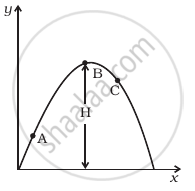
A particle is projected in air at some angle to the horizontal, moves along parabola as shown in figure, where x and y indicate horizontal and vertical directions, respectively. Show in the diagram, direction of velocity and acceleration at points A, B and C.
Solution
In projectile motion, horizontal component of velocity will always be constant and acceleration is always vertically downward and is equal to g. The direction of velocity will always be tangential to the curve in the direction of motion.
As shown in the diagram in which a particle is projected at an angle of θ.
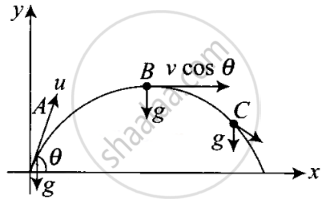
vx = Horizontal component of velocity
= v cos θ = constant
vy = Vertical component of velocity
= v sin θ
APPEARS IN
RELATED QUESTIONS
Show that for a projectile the angle between the velocity and the x-axis as a function of time is given by
`theta(t) =tan^(-1) ((v_(0y) - "gt")/v_(o x))`
Show that the projection angle `theta_o` for a projectile launched from the origin is given by
`theta_o =tan^(-1) ((4h_m)/R)`
Where the symbols have their usual meaning
A ball rolls of the top of the stairway with a horizontal velocity u ms−1. If the steps are h m high and b m wide, the ball will hit the edge of the nth step, if:
A car starts from rest and accelerates at 5 m/s2. At t = 4 s, a ball is dropped out of a window by a person sitting in the car. What is the velocity and acceleration of the ball at t = 6 s? (Take g = 10 m/s2)
A football is kicked into the air vertically upwards. What is its acceleration?
In dealing with motion of projectile in air, we ignore effect of air resistance on motion. This gives trajectory as a parabola as you have studied. What would the trajectory look like if air resistance is included? Sketch such a trajectory and explain why you have drawn it that way.
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
The trajectories of the two projectiles are shown in the figure. Let T1 and T2 be the time periods and u1 and u2 be their speeds of projection. Then ______.