Advertisements
Advertisements
प्रश्न
A particle is projected in air at an angle β to a surface which itself is inclined at an angle α to the horizontal (Figure).
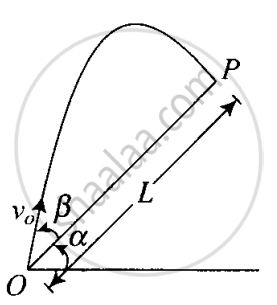
- Find an expression of range on the plane surface (distance on the plane from the point of projection at which particle will hit the surface).
- Time of flight.
- β at which range will be maximum.
उत्तर
a. Since we have, `x = L`
`u_x = v_x = v_0 cos β`
`a_x = - g sin α`
And `t = T = (2v_0 sin β)/(g cos α)`
Hence, `s = u_xt + 1/2 a_xt^2`
Gives us, L = `v_0 cos B * T + 1/2 (- g sin α) T^2`
= `T[v_0 cos β - 1/2 g sin α T]`
Putting `T = (2v_0 sin β)/(g cos α)` given us,
⇒ `L = (2v_0^2 sin β)/(g cos^2 α) cos(α + β)`
That is the required range.
b. Let us first calculate the time of flight.
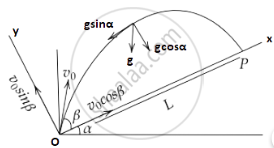
We have,
⇒ `s = ut + 1/2 gt^2`
Where, `s = 0`
`u = u_y = v_0 sin β`
`g = g_y = - g cos α, t = T`
Hence, ⇒ `0 = v_0 sin β (T) + 1/2 (-g cos α)T^2`
i.e. ⇒ `T[v_0 sin β - T g/2 cos α]` = 0
So either T is zero or `v_0 sin β - T g/2 cos α`
That gives the time of flight as `T = (2v_0 sin β)/(g cos α)`
c. Let us consider the equation `Z = sin β cos(α + β)`
We can write `Z = sin β cos(α + β) = 1/2 [sin(2β + α) - sin α]`
Now for Z to be maximum, it must have `sin(2β + α) = 1`
i.e. `sin(2β + α) = sin 90^circ`
That gives, `2β + α = 90^circ`
Hence, `β = (90^circ - α)/2` or `β = pi/4 - α/2`
APPEARS IN
संबंधित प्रश्न
A bullet fired at an angle of 30° with the horizontal hits the ground 3.0 km away. By adjusting its angle of projection, can one hope to hit a target 5.0 km away? Assume the muzzle speed to the fixed, and neglect air resistance.
A cricket ball thrown across a field is at heights h1 and h2 from the point of projection at times t1 and t2 respectively after the throw. The ball is caught by a fielder at the same height as that of projection. The time of flight of the ball in this journey is
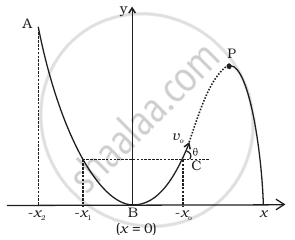
A particle slides down a frictionless parabolic (y = x2) track (A – B – C) starting from rest at point A (Figure). Point B is at the vertex of parabola and point C is at a height less than that of point A. After C, the particle moves freely in air as a projectile. If the particle reaches highest point at P, then
A cricket fielder can throw the cricket ball with a speed vo. If he throws the ball while running with speed u at an angle θ to the horizontal, find
- the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.
- what will be time of flight?
- what is the distance (horizontal range) from the point of projection at which the ball will land?
- find θ at which he should throw the ball that would maximise the horizontal range as found in (iii).
- how does θ for maximum range change if u > vo, u = vo, u < vo?
- how does θ in (v) compare with that for u = 0 (i.e.45)?
The minimum speed in m/s with which a projectile must be thrown from origin at ground so that it is able to pass through a point P (30 m, 40 m) is ______. (g = 10 m/s2)
A body is thrown from a point with speed 50 m/s at an angle 37° with horizontal. When it has moved a horizontal distance of 80 m then its distance from point of projection is ______.
Two stones are projected with the same speed but making different angles with the horizontal. Their ranges are equal. If the angle of projection of one is `pi/3` and its maximum height is y1 then the maximum height of the other will be ______.
For a projectile thrown into space with a speed v, the horizontal range is `(sqrt3"v"^2)/(2"g")`. The vertical range is `"v"^2/(8"g")`. The angle which the projectile makes with the horizontal initially is ______.
A person standing on a truck moving with a uniform velocity of 14.7 ms-1 on a horizontal road throws a ball in such a way that it returns to him after 4s. Find the speed and angle of projection as seen by a man on the road ______.
An object is projected in the air with initial velocity u at an angle θ. The projectile motion is such that the horizontal range R, is maximum.
Another object is projected in the air with a horizontal range half of the range of first object. The initial velocity remains same in both the case. The value of the angle of projection, at which the second object is projected, will be ______ degree.
